题目内容
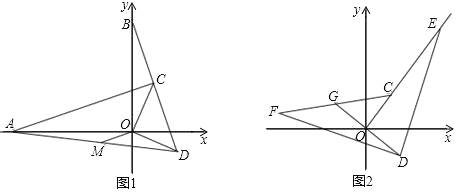
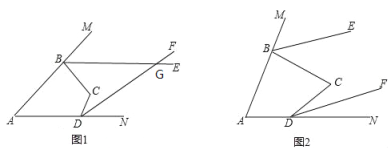
【题目】如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β
(1)如图,若α+β=120°,求∠MBC+∠NDC的度数;
(2)如图,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;
(3)如图,若α=β,判断BE、DF的位置关系,并说明理由.
【答案】(1)120°; (2)β﹣α=60° 理由见解析;(3)平行,理由见解析.
【解析】
(1)利用四边形的内角和求出∠ABC与∠ADC的和,利用角平分线的定义以及α+β=120°推导即可;
(2)由(1)得,∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBG+∠CDG=![]() (α+β),在△BCD中利用三角形的内角和定理得∠BDC+∠CDB =180°﹣β,在△BDG中利用三角形的内角和定理得出关于α、β的等式整理即可得出结论;
(α+β),在△BCD中利用三角形的内角和定理得∠BDC+∠CDB =180°﹣β,在△BDG中利用三角形的内角和定理得出关于α、β的等式整理即可得出结论;
(3)延长BC交DF于H,由(1)得∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBE+∠CDH=![]() (α+β),利用三角形的外角的性质得∠CDH=β﹣∠DHB,然后代入∠CBE+∠CDH=
(α+β),利用三角形的外角的性质得∠CDH=β﹣∠DHB,然后代入∠CBE+∠CDH=![]() (α+β)计算即可得出一组内错角相等.
(α+β)计算即可得出一组内错角相等.
(1)解:(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,
∵α+β=120°,
∴∠MBC+∠NDC=120°;
(2)β﹣α=60°
理由:如图1,连接BD,
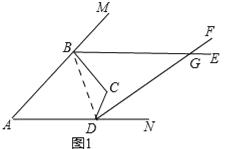
由(1)得,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=![]() ∠MBC,∠CDG=
∠MBC,∠CDG=![]() ∠NDC,
∠NDC,
∴∠CBG+∠CDG=![]() ∠MBC+
∠MBC+![]() ∠NDC=
∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
在△BCD中,∠BDC+∠CDB=180°﹣∠BCD=180°﹣β,
在△BDG中, ∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴![]() (α+β)+180°﹣β+30°=180°,
(α+β)+180°﹣β+30°=180°,
∴β﹣α=60°,
(3)平行,
理由:如图2,延长BC交DF于H,
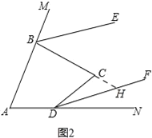
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=![]() ∠MBC,∠CDH=
∠MBC,∠CDH=![]() ∠NDC,
∠NDC,
∴∠CBE+∠CDH=![]() ∠MBC+
∠MBC+![]() ∠NDC=
∠NDC=![]() (∠MBC+∠NDC)=
(∠MBC+∠NDC)=![]() (α+β),
(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,
∴∠CBE+β﹣∠DHB=![]() (α+β),
(α+β),
∵α=β,
∴∠CBE+β﹣∠DHB=![]() (β+β)=β,
(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案【题目】某品牌运动鞋经销商购进A、B两种新式运动鞋,按标价售出后可获利48000元.已知购进A种运动鞋的数量是B种运动鞋数量的2倍,这两种运动鞋的进价、标价如下表所示.
款式 价格 | A | B |
进价(元/双) | 100 | 120 |
标价(元/双) | 250 | 300 |
(1)这两种运动鞋各购进多少双?
(2)如果A种运动鞋按标价9折出售,B种运动鞋按标价8折出售,那么这批运动鞋全部售出后,经销商所获利润比按标价出售少收入多少元?