题目内容
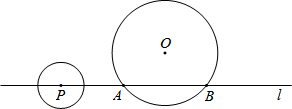（2013•泰州）如图，⊙O的半径为4cm，直线l与⊙O相交于A、B两点，AB=4| 3 |
d＞5或2≤d＜3
d＞5或2≤d＜3
．分析：根据两圆内切和外切时，求出两圆圆心距，进而得出d的取值范围．
解答：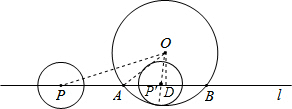
解：连接OP、OA，
∵⊙O的半径为4cm，1cm为半径的⊙P，⊙P与⊙O没有公共点，
∴d＞5时，两圆外离，
当两圆内切时，过点O作OD⊥AB于点D，
OP′=4-1=3cm，OD=
=2（cm），
∴以1cm为半径的⊙P与⊙O没有公共点时，2≤d＜3，
故答案为：d＞5或2≤d＜3．
解：连接OP、OA，∵⊙O的半径为4cm，1cm为半径的⊙P，⊙P与⊙O没有公共点，
∴d＞5时，两圆外离，
当两圆内切时，过点O作OD⊥AB于点D，
OP′=4-1=3cm，OD=
42-(2
|
∴以1cm为半径的⊙P与⊙O没有公共点时，2≤d＜3，
故答案为：d＞5或2≤d＜3．
点评：此题主要考查了圆与圆的位置关系，根据图形进行分类讨论得出是解题关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
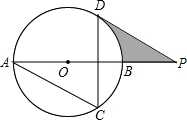（2013•泰州）如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
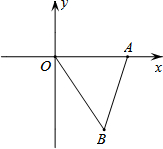（2013•泰州）如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，-3），△AB′O′是△ABO关于的A的位似图形，且O′的坐标为（-1，0），则点B′的坐标为
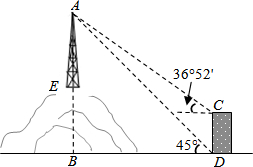（2013•泰州）如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）
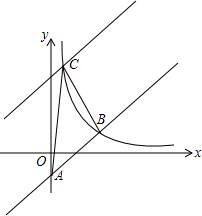（2013•泰州） 如图，在平面直角坐标系中直线y=x-2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．