题目内容
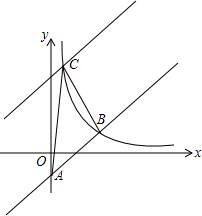 (2013•泰州) 如图,在平面直角坐标系中直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(2013•泰州) 如图,在平面直角坐标系中直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).(1)求反比例函数的关系式;
(2)将直线y=x-2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
分析:(1)设反比例解析式为y=
,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)过C作CD垂直于y轴,过B作BE垂直于y轴,设y=x-2平移后解析式为y=x+b,C坐标为(a,a+b),三角形ABC面积=梯形BEDC面积+三角形ABE面积-三角形ACD面积,由已知三角形ABC面积列出关系式,将C坐标代入反比例解析式中列出关系式,两关系式联立求出b的值,即可确定出平移后直线的解析式.
| k |
| x |
(2)过C作CD垂直于y轴,过B作BE垂直于y轴,设y=x-2平移后解析式为y=x+b,C坐标为(a,a+b),三角形ABC面积=梯形BEDC面积+三角形ABE面积-三角形ACD面积,由已知三角形ABC面积列出关系式,将C坐标代入反比例解析式中列出关系式,两关系式联立求出b的值,即可确定出平移后直线的解析式.
解答: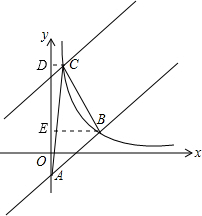 解:(1)将B坐标代入直线y=x-2中得:m-2=2,
解:(1)将B坐标代入直线y=x-2中得:m-2=2,
解得:m=4,
则B(4,2),即BE=4,OE=2,
设反比例解析式为y=
,
将B(4,2)代入反比例解析式得:k=8,
则反比例解析式为y=
;
(2)设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x-2,令x=0求出y=-2,得到OA=2,
过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8,
∵S△ABC=S梯形BCDE+S△ABE-S△ACD=18,
∴
×(a+4)×(a+b-2)+
×(2+2)×4-
×a×(a+b+2)=18,
解得:a+b=8,
∴a=1,b=7,
则平移后直线解析式为y=x+7.
 解:(1)将B坐标代入直线y=x-2中得:m-2=2,
解:(1)将B坐标代入直线y=x-2中得:m-2=2,解得:m=4,
则B(4,2),即BE=4,OE=2,
设反比例解析式为y=
| k |
| x |
将B(4,2)代入反比例解析式得:k=8,
则反比例解析式为y=
| 8 |
| x |
(2)设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x-2,令x=0求出y=-2,得到OA=2,
过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8,
∵S△ABC=S梯形BCDE+S△ABE-S△ACD=18,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:a+b=8,
∴a=1,b=7,
则平移后直线解析式为y=x+7.
点评:此题考查了一次函数与反比例函数的交点问题,涉及的知识有:一次函数与坐标轴的交点,待定系数法求函数解析式,三角形、梯形的面积求法,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
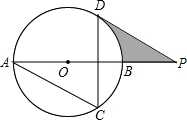 (2013•泰州)如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(2013•泰州)如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.