题目内容
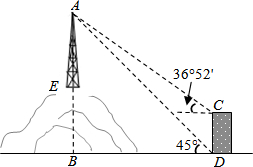（2013•泰州）如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）分析：根据楼高和山高可求出EF，继而得出AF，在Rt△AFC中表示出CF，在Rt△ABD中表示出BD，根据CF=BD可建立方程，解出即可．
解答：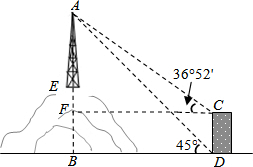
解：如图，过点C作CF⊥AB于点F．
设塔高AE=x，
由题意得，EF=BE-CD=56-27=29m，AF=AE+EF=（x+29）m，
在Rt△AFC中，∠ACF=36°52′，AF=（x+29）m，
则CF=
≈
=
x+
，
在Rt△ABD中，∠ADB=45°，AB=x+56，
则BD=AB=x+56，
∵CF=BD，
∴x+56=
x+
，
解得：x=52，
答：该铁塔的高AE为52米．
解：如图，过点C作CF⊥AB于点F．设塔高AE=x，
由题意得，EF=BE-CD=56-27=29m，AF=AE+EF=（x+29）m，
在Rt△AFC中，∠ACF=36°52′，AF=（x+29）m，
则CF=
| AF |
| tan36°52′ |
| x+29 |
| 0.75 |
| 4 |
| 3 |
| 116 |
| 3 |
在Rt△ABD中，∠ADB=45°，AB=x+56，
则BD=AB=x+56，
∵CF=BD，
∴x+56=
| 4 |
| 3 |
| 116 |
| 3 |
解得：x=52，
答：该铁塔的高AE为52米．
点评：本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，注意利用方程思想求解，难度一般．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
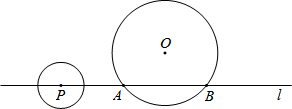（2013•泰州）如图，⊙O的半径为4cm，直线l与⊙O相交于A、B两点，AB=4
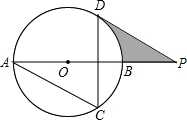（2013•泰州）如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
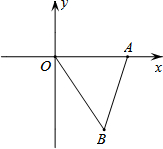（2013•泰州）如图，平面直角坐标系xOy中，点A、B的坐标分别为（3，0）、（2，-3），△AB′O′是△ABO关于的A的位似图形，且O′的坐标为（-1，0），则点B′的坐标为
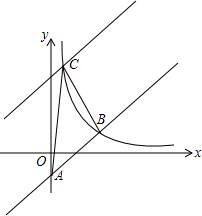（2013•泰州） 如图，在平面直角坐标系中直线y=x-2与y轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．