题目内容
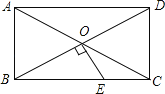
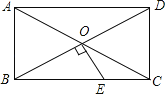
【题目】如图,ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
首先证明四边形ABCD是矩形,在RT△BOE中,易知BE=2EO,只要证明EO=EC即可.
∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵△ABO是等边三角形,
∴AO=BO=AB,
∴AO=OC=BO=OD,
∴AC=BD,
∴四边形ABCD是矩形.
∴OB=OC,∠ABC=90°,
∵△ABO是等边三角形,
∴∠ABO=60°,
∴∠OBC=∠OCB=30°,∠BOC=120°,
∵BO⊥OE,
∴∠BOE=90°,∠EOC=30°,
∴∠EOC=∠ECO,
∴EO=EC,
∴BE=2EO=2CE,
∵CD=1,
∴BC=![]() CD=
CD=![]() ,
,
∴EC=![]() BC=
BC=![]() ,
,
故选:D.

练习册系列答案
相关题目
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
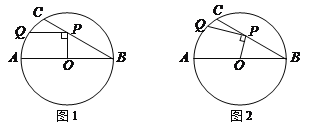
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
【题目】某商场计划用3 800元购进节能灯120只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?