Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľĘŔ£¨![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £ģ∂ĮĶ„
£ģ∂ĮĶ„![]() ‘ŕ
‘ŕ![]() ĶńĪŖ…Ōįī
ĶńĪŖ…Ōįī![]() Ķń¬∑ŌŖ‘»ňŔ“∆∂Į£¨ĶĪĶ„
Ķń¬∑ŌŖ‘»ňŔ“∆∂Į£¨ĶĪĶ„![]() ĶĹīÔ
ĶĹīÔ![]() Ķ„ ĪÕ£÷Ļ“∆∂Į£Ľ∂ĮĶ„
Ķ„ ĪÕ£÷Ļ“∆∂Į£Ľ∂ĮĶ„![]() “‘
“‘![]() ĶńňŔ∂»‘ŕ
ĶńňŔ∂»‘ŕ![]() ĶńĪŖ…Ōįī
ĶńĪŖ…Ōįī![]() Ķń¬∑ŌŖ‘»ňŔ“∆∂Į£¨ĶĪĶ„
Ķń¬∑ŌŖ‘»ňŔ“∆∂Į£¨ĶĪĶ„![]() ĶĹīÔ
ĶĹīÔ![]() Ķ„ ĪÕ£÷Ļ“∆∂Į£ģ“—÷™Ķ„
Ķ„ ĪÕ£÷Ļ“∆∂Į£ģ“—÷™Ķ„![]() °ĘĶ„
°ĘĶ„![]() Õ¨ ĪŅ™ ľ“∆∂Į£¨Õ¨ ĪÕ£÷Ļ“∆∂Į(ľīÕ¨ ĪĶĹīÔłų◊‘Ķń÷’÷ĻőĽ÷√)£ģ…Ť∂ĮĶ„
Õ¨ ĪŅ™ ľ“∆∂Į£¨Õ¨ ĪÕ£÷Ļ“∆∂Į(ľīÕ¨ ĪĶĹīÔłų◊‘Ķń÷’÷ĻőĽ÷√)£ģ…Ť∂ĮĶ„![]() “∆∂ĮĶń Īľšő™
“∆∂ĮĶń Īľšő™![]() £¨
£¨![]() Ķń√śĽżő™
Ķń√śĽżő™![]() £¨
£¨![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ»ÁÕľĘŕňý ĺ£ģ
ĶńļĮ żĻōŌĶ»ÁÕľĘŕňý ĺ£ģ
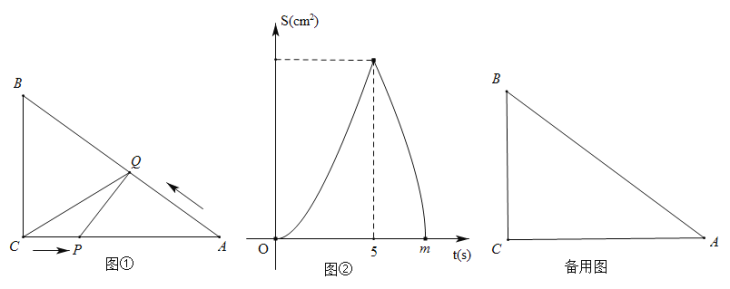
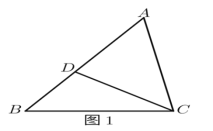
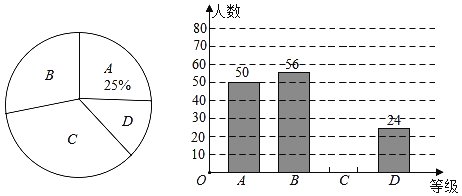
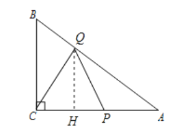
(1)ÕľĘŔ÷–![]() °°°°
°°°°![]() £¨ÕľĘŕ÷–
£¨ÕľĘŕ÷–![]() °°°°
°°°°![]() £Ľ
£Ľ
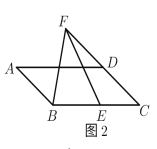
(2)«ů![]() ”Ž
”Ž![]() ĶńļĮ żĪŪīÔ Ĺ£Ľ
ĶńļĮ żĪŪīÔ Ĺ£Ľ
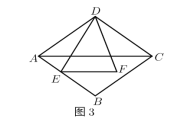
(3)ĶĪ![]() ő™ļő÷Ķ Ī£¨
ő™ļő÷Ķ Ī£¨![]() ő™Ķ»—Ł»żĹ«–ő£ģ
ő™Ķ»—Ł»żĹ«–ő£ģ
°ĺīūįł°Ņ£®1£©10£¨15£Ľ£®2£©ľŻŌÍĹ‚£Ľ£®3£©ľŻŌÍĹ‚
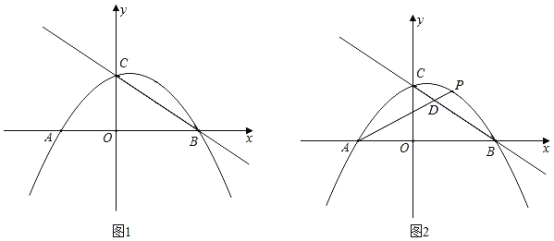
°ĺĹ‚őŲ°Ņ
![]() £¨łýĺ›
£¨łýĺ›![]() £¨
£¨![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() £¨ĹÝ∂ÝĶ√ĶĹ∂ĮĶ„PĶńňŔ∂»ő™£ļ
£¨ĹÝ∂ÝĶ√ĶĹ∂ĮĶ„PĶńňŔ∂»ő™£ļ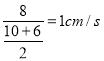 £¨ľīŅ…Ķ√ĶĹ
£¨ľīŅ…Ķ√ĶĹ![]() £Ľ
£Ľ
£®2£©ĶĪ![]() Ī£¨ĻżĶ„
Ī£¨ĻżĶ„![]() ◊ų
◊ų![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() £¨łýĺ›
£¨łýĺ›![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() £¨
£¨![]() £¨ĹÝ∂ÝĶ√ĶĹ
£¨ĹÝ∂ÝĶ√ĶĹ![]() £¨
£¨![]() £ĽĶĪ
£ĽĶĪ![]() Ī£¨
Ī£¨![]() £Ľ
£Ľ
£®3£©ĶĪ![]() Ī£¨Ķ„
Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō£¨łýĺ›
…Ō£¨łýĺ›![]() £¨
£¨![]() £¨
£¨![]() £¨»Ű
£¨»Ű![]() ő™Ķ»—Ł»żĹ«–ő£¨‘Ú
ő™Ķ»—Ł»żĹ«–ő£¨‘Ú![]() £¨łýĺ›
£¨łýĺ›![]() £¨
£¨![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() £¨łýĺ›
£¨łýĺ›![]() ľīŅ…«ůĹ‚£ĽĶĪ
ľīŅ…«ůĹ‚£ĽĶĪ![]() Ī£¨Ķ„
Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō£¨łýĺ›
…Ō£¨łýĺ›![]() £¨»Ű
£¨»Ű![]() ő™Ķ»—Ł»żĹ«–ő£¨‘Ú
ő™Ķ»—Ł»żĹ«–ő£¨‘Ú![]() £¨Ķ√ĶĹ
£¨Ķ√ĶĹ![]() £¨ľīŅ…«ůĹ‚£ģ
£¨ľīŅ…«ůĹ‚£ģ
Ĺ‚£ļ£®1£©![]()
°Ŗ![]() £¨
£¨![]()
°ŗ![]()
°ŗ∂ĮĶ„PĶńňŔ∂»ő™£ļ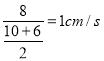
°ŗ![]()
Ļ īūįłő™£ļ10£¨15£ģ
£®2£©ĶĪ![]() Ī£¨ĻżĶ„
Ī£¨ĻżĶ„![]() ◊ų
◊ų![]() £¨īĻ◊„ő™
£¨īĻ◊„ő™![]() £¨
£¨
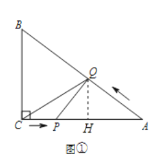
°Ŗ![]()
°ŗ![]()
°ŗ![]()
°ŗ![]()
°ŗ![]()
°ŗ![]() £Ľ
£Ľ
ĶĪ![]() Ī£¨
Ī£¨![]() £Ľ
£Ľ
£®3£©ĶĪ![]() Ī£¨Ķ„
Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō.
…Ō.
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() »Ű
»Ű![]() ő™Ķ»—Ł»żĹ«–ő£¨‘Ú
ő™Ķ»—Ł»żĹ«–ő£¨‘Ú![]() .
.
![]() £¨
£¨![]() £¨
£¨![]() .
.
![]() £¨
£¨![]() £Ľ
£Ľ
ĶĪ![]() Ī£¨Ķ„
Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() …Ō.
…Ō.
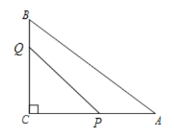
![]() ,
,![]() »Ű
»Ű![]() ő™Ķ»—Ł»żĹ«–ő£¨‘Ú
ő™Ķ»—Ł»żĹ«–ő£¨‘Ú![]() .
.
![]() £¨
£¨![]() .
.

 √Ż–£√Ż ¶Ňŗ”Ň◊ų“ĶĪĺľ”ļň–ń ‘ĺŪŌĶŃ–īūįł
√Ż–£√Ż ¶Ňŗ”Ň◊ų“ĶĪĺľ”ļň–ń ‘ĺŪŌĶŃ–īūįł »ę≥ŐĹūĺŪŌĶŃ–īūįł
»ę≥ŐĹūĺŪŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ∂ĢīőļĮ ż![]() £®
£®![]() £¨
£¨![]() £¨
£¨![]() «≥£ ż£¨
«≥£ ż£¨![]() £©Ķń◊‘ĪšŃŅx”ŽļĮ ż÷ĶyĶń≤Ņ∑÷∂‘”¶÷Ķ»ÁŌ¬ĪŪ£ļ
£©Ķń◊‘ĪšŃŅx”ŽļĮ ż÷ĶyĶń≤Ņ∑÷∂‘”¶÷Ķ»ÁŌ¬ĪŪ£ļ
| °≠ | -1 | 0 | 1 | 3 | °≠ |
| °≠ |
| 3 |
| 3 | °≠ |
«“ĶĪ![]() Ī£¨”Ž∆š∂‘”¶ĶńļĮ ż÷Ķ
Ī£¨”Ž∆š∂‘”¶ĶńļĮ ż÷Ķ![]() £ģ”–Ō¬Ń–ĹŠ¬Ř£ļĘŔ
£ģ”–Ō¬Ń–ĹŠ¬Ř£ļĘŔ![]() £ĽĘŕ3 «Ļō”ŕ
£ĽĘŕ3 «Ļō”ŕ![]() Ķń∑Ĺ≥Ő
Ķń∑Ĺ≥Ő![]() Ķń“ĽłŲłý£ĽĘŘ
Ķń“ĽłŲłý£ĽĘŘ![]() £ģ∆š÷–£¨’ż»∑ĹŠ¬ŘĶńłŲ ż «£® £©
£ģ∆š÷–£¨’ż»∑ĹŠ¬ŘĶńłŲ ż «£® £©
A.0B.1C.2/span>D.3