Question

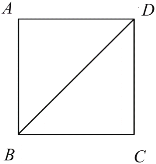
【题目】如图，正方形中，，点是正方形所在平面内一动点，满足．

（1）当点在直线上方且时，求证：；

（2）若，求点到直线的距离；

（3）记，在点运动过程中，是否存在最大值或最小值？若存在，求出其值，若不存在，说明理由．

Answer 1

【答案】（1）见解析；（2）或；（3）当时，最小值为．当点在直线下方时，有最大值

【解析】

（1）利用勾股定理的逆定理证明△ADQ是等腰直角三角形即可解决问题．
（2）如图2中，由题意点Q是以D为圆心，DQ为半径的圆和以BD为直径的圆的交点（有两种情形，图中Q，Q′）．连接BQ，BQ′，过点A作AH⊥BQ于H，过点A作AH′⊥BQ′于H，AH′交BQ于J．解直角三角形求出AH，BH即可解决问题．
（3）如图3-1中，当AQ＜BQ时，过点A作QJ⊥AB交BA的延长线于J．AQ2-BQ2=JQ2+AJ2-（JQ2+BJ2）=AJ2-BJ2=（AJ+BJ）（JA-BJ）=-AB（2JA+AB）=（2JA+），观察图象可知，当JA的值最大时，AQ2-BQ2的值最小，此时点Q在CD的延长线上．如图3-2中，当QA＞QB时，过点A作QJ⊥AB交BA的延长线于J．AQ2-BQ2=JQ2+AJ2-（JQ2+BJ2）=AJ2-BJ2=（AJ+BJ）（JA-BJ）=AB（AJ-BJ），观察图象可知，当JA-JB的值最大时，AQ2-BQ2的值最大，此时点Q在线段CD上．

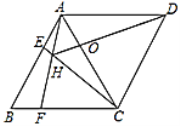
解：（1）证明：如图1中，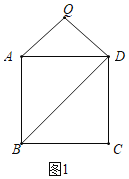

∵AQ=DQ=1，AD=，
∴AQ2+DQ2=AD2，
∴∠Q=90°，
∴∠QAD=∠ADQ=45°，
∵四边形ABCD是正方形，
∴∠ADB=45°，
∴∠ADB=∠QAD，
∴AQ∥BD．
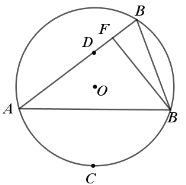
（2）解：如图2中，由题意点Q是以D为圆心，DQ为半径的圆和以BD为直径的圆的交点（有两种情形，图中Q，Q′）．

连接BQ，BQ′，过点A作AH⊥BQ于H，过点A作AH′⊥BQ′于H，AH′交BQ于J．
∵BD=AD=2，QD=1，
∴BQ=2DQ，
∴∠QBD=30°，同法可得∠DBQ′=30°，
∵四边形ABCD是正方形，
∴∠ABD=∠CBD=45°，
∴∠ABQ=∠CBQ′=15°，
∴∠ABH′=75°，∠BAJ=15°，
∴∠JAB=∠JBA=15°，
∴∠AJH=∠JAB+∠JBA=30°，

设AH=a，则AJ=JB=2AH=2a，JH=，
在Rt△ABH中，则有2=a2+（2a+）2，
解得a=，
∴AH=，BH=，
∵∠AHB=∠AH′B=90°，∠ABH=∠BAH′，AB=BA，
∴△AHB≌△BH′A（AAS），
∴AH′=BH=，
∴点A到直线BQ的距离为或．
（3）解：如图3-1中，当AQ＜BQ时，过点A作QJ⊥AB交BA的延长线于J．

∵AQ2-BQ2=JQ2+AJ2-（JQ2+BJ2）=AJ2-BJ2=（AJ+BJ）（JA-BJ）=-AB（2JA+AB）=（2JA+），
观察图象可知，当JA的值最大时，AQ2-BQ2的值最小，此时点Q在CD的延长线上，

最小值=（2+）=．
如图3-2中，当QA＞QB时，过点A作QJ⊥AB交BA的延长线于J．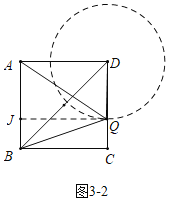

∵AQ2-BQ2=JQ2+AJ2-（JQ2+BJ2）=AJ2-BJ2=（AJ+BJ）（JA-BJ）=AB（AJ-BJ），
观察图象可知，当JA-JB的值最大时，AQ2-BQ2的值最大，此时点Q在线段CD上，

最大值=（1-+1）=2-2．