题目内容
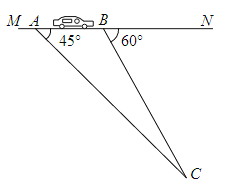
【题目】如图,在某笔直路段MN内小车行驶的最高限速60千米/小时.交通部门为了检测车辆是否在此路段超速行驶,在公路MN旁设立了观测点C,已知∠CAN=45°,∠CBN=60°,BC=120米.
(1)求测速点C到该公路的距离;
(2)若测得一小车从A点到达点B行驶了3秒,请通过计算判断此车是否超速.(参考数据:![]() ,
,![]() )
)
【答案】此车没有超速.
【解析】分析:(1)根据题意结合锐角三角函数关系得出CE即可;
(2)求出BE、AB的长,进而求出汽车的速度,即可得出答案.
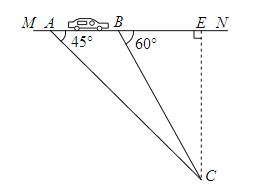
详解:(1)过C作CE⊥MN,垂足为E,如图所示:
∵∠CBN=60°,BC=200m,∴CE=BCsin60°=200×![]() =100
=100![]() (m),
(m),
即观测点C到公路MN的距离为100![]() m;
m;
(2)该汽车没有超速.理由如下:
∵BE=BCcos60°=100(米).
∵∠CAN=45°,∴AE=CE=100![]() m,∴AB=100
m,∴AB=100![]() ﹣100≈73(m),∴车速为
﹣100≈73(m),∴车速为![]() =14.6m/s.
=14.6m/s.
∵60千米/小时=![]() m/s.
m/s.
又∵14.6<![]() ,∴该汽车没有超速.
,∴该汽车没有超速.

练习册系列答案
相关题目