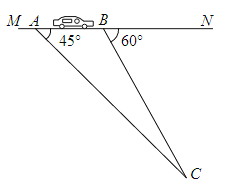
题目内容
【题目】如图,在△ABC中,AB = AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点,请写出图中两组全等的三角形,并选出其中一组加以证明.(要求:写出证明过程中的重要依据)
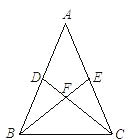
【答案】△ABE≌△ACD,△BCD≌△CBE或△BFD≌△CFE(写出两个即可),选择一个证明即可.
【解析】利用全等三角形的判定定理证明方法,选择证明即可.
△ABE≌△ACD,△BCD≌△CBE或△BFD≌△CFE(写出两个即可).
(1)选△ABE≌△ACD,
证明:∵点D、E分别是AB、AC的中点,
∴AD=![]() AB,AE=
AB,AE=![]() AC,
AC,
又∵AB=AC,∴AD=AE,
在△ABE和△ACD中, 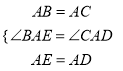
∴△ABE≌△ACD(SAS)
(2)选△BCD≌△CBE.
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵点D、E分别是AB、AC的中点,
∴BD=![]() AB,CE=
AB,CE=![]() AC,∴BD=CE,
AC,∴BD=CE,
在△BCD和△CBE中, 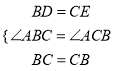 ,
,
∴△BCD≌△CBE.
(3)选△BFD≌△CFE.
证明:∵点D、E分别是AB、AC的中点,
∴AD=![]() AB,AE=
AB,AE=![]() AC.
AC.
在△ABE和△ACD中, 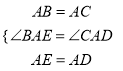 ,
,
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD(全等三角形对应角相等)
∵点D、E分别是AB、AC的中点,
∴BD=![]() AB,CE=
AB,CE=![]() AC,
AC,
∴BD=CE,
在△BFD和△CFE中, 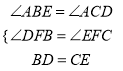 ,
,
∴△BFD≌△CFE(AAS).

【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?