Question

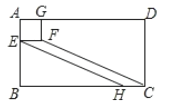
【题目】如图，四边形ABCD是长方形，四边形AEFG是正方形，点E，G分别在AB，AD上，连接FC，过点E作EH∥FC交BC于点H．若∠BCF=30°，CD=4，CF=6，则正方形AEFG的面积为（　　）

A. 1B. 2C. 3D. 4

Answer 1

【答案】A

【解析】

由矩形和正方形的性质得出AD∥EF∥BC，AB=CD=4，∠B=90°，证出四边形EFCH平行四边形，∠BHE=∠BCF=30°，得出EH=CF=6，由含30°角的直角三角形的性质求出BE=3，得出AE的长，即可得出正方形的面积．

∵四边形ABCD是矩形，四边形AEFG是正方形，
∴AD∥EF∥BC，AB=CD=4，∠B=90°，
又∵EH∥FC，
∴四边形EFCH平行四边形，∠BHE=∠BCF=30°，
∴EH=CF=6，
∴BE=EH=3，
∴AE=AB-BE=4-3=1，
∴正方形AEFG的面积=AE2=1；
故选：A．