Question

【题目】如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D．

（1）求证：∠PCD＝∠PDC；

（2）求证：OP是线段CD的垂直平分线.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）由角平分线的性质可得PC=PD，即可证明∠PCD＝∠PDC；（2）先证明△OCP≌△ODP，由此可得OC＝OD，进而证明点O在CD的垂直平分线上，由（1）PC=PD可得点P也在CD的垂直平分线上，所以OP是线段CD的垂直平分线.

试题解析：

（1）∵OP是∠AOB的角平分线，PC⊥OA，PD⊥OB，

∴PC＝PD，

∴∠PCD＝∠PDC；

（2）∵OP是∠AOB的角平分线，

∴∠COP＝∠DOP，

∵PC⊥OA，PD⊥OB，

∴∠OCP＝∠ODP＝90°，

在△OCP和△ODP中，

，

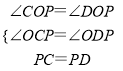∴△OCP≌△ODP（AAS），

∴OC＝OD，

∴点O在CD的垂直平分线上，

∵PC＝PD，

∴点P在CD的垂直平分线上，

∴OP是CD的垂直平分线.