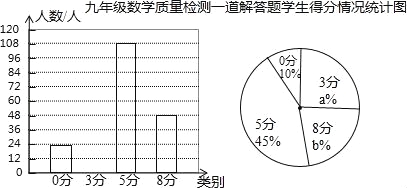
��Ŀ����
����Ŀ��ij��˾�ƻ�����A��B���ּ�������100����Ҫ��A�ּ���������������B�ֵ�![]() ���Ҳ�����B�ֵ�
���Ҳ�����B�ֵ�![]() ����֪A��B���ּ������ĵ��۷ֱ���150Ԫ/����100Ԫ/�����蹺��A�ּ�����x����
����֪A��B���ּ������ĵ��۷ֱ���150Ԫ/����100Ԫ/�����蹺��A�ּ�����x����
��1����ƻ����������ּ������������y��Ԫ����x�ĺ�����ϵʽ��
��2���ʸù�˾���ƻ����������ּ������ж����ַ�����
��3�������г����鲨����ʵ�ʹ���ʱ��A�ּ����������µ���3m��m��0��Ԫ/����ͬʱB�ּ����������ϵ���2mԪ/������ʱ���������ּ������������ٷ���Ϊ12150Ԫ����m��ֵ��
���𰸡���1��y��50x+10000����2���������ּ�������6�ַ�������2��m��11.5ʱ�����������ּ������������ٷ���Ϊ12150Ԫ��
��������
��1�����ݵ��۳������������ܼۣ���ʾ������A��B���ּ��������ܼۣ�Ȼ������Ӿ����ܹ�����Ҫ�ķ��ã�
��2��������Ŀ����A�ּ���������������B�ֵ�![]() ���Ҳ�����B�ֵ�
���Ҳ�����B�ֵ�![]() �����Թ�������ʽ�飬�ӳ�����ʽ��Ϳ������x��ȡֵ��Χ���Ӷ��õ�������
�����Թ�������ʽ�飬�ӳ�����ʽ��Ϳ������x��ȡֵ��Χ���Ӷ��õ�������
��3��������Ŀ�������������������ּ������������ٷ���Ϊ12150Ԫ�ķ��̣����m���ɣ�
��1������ã�
y��150x+100��100��x����50x+10000��
��2����A�ּ���������������B�ֵ�![]() ���Ҳ�����B�ֵ�
���Ҳ�����B�ֵ�![]() �ã�
�ã�
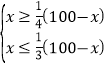 ����ã�20��x��25��
����ã�20��x��25��
�����ּ������ù����У�
����һ��A�ּ�����20����B�ּ�����80����
��������A�ּ�����21����B�ּ�����79����
��������A�ּ�����22����B�ּ�����78����
�����ģ�A�ּ�����23����B�ּ�����77����
�����壺A�ּ�����24����B�ּ�����76����
��������A�ּ�����25����B�ּ�����75����
���ϣ��������ּ�������6�ַ�����
��3����150��3m��x+��100+2m����100��x����12150��
150x��3mx+10000��100x+200m��2mx��12150��
��50��5m��x��2150��200m��
��x��20ʱ���������٣�
��20��50��5m����2150��200m��
���m��11.5��
��m��11.5ʱ�����������ּ������������ٷ���Ϊ12150Ԫ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�