题目内容
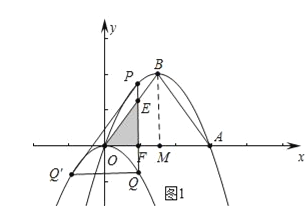
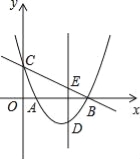
【题目】如图,在平面直角坐标系中.有抛物线![]() 和
和![]() .抛物线
.抛物线![]() 经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线
经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线![]() 上一点,且在x轴上方.过点P作x轴的垂线交抛物线
上一点,且在x轴上方.过点P作x轴的垂线交抛物线![]() 于点Q.过点Q作PQ的垂线交抛物线
于点Q.过点Q作PQ的垂线交抛物线![]() 于点
于点![]() (不与点Q重合),连结
(不与点Q重合),连结![]() .设点P的横坐标为m.
.设点P的横坐标为m.

(1)求a的值;
(2)当抛物线![]() 经过原点时,设△
经过原点时,设△![]() 与△OAB重叠部分图形的周长为l.
与△OAB重叠部分图形的周长为l.
①求![]() 的值;
的值;
②求l与m之间的函数关系式;
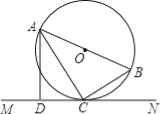
(3)当h为何值时,存在点P,使以点O、A、Q、![]() 为顶点的四边形是轴对称图形?直接写出h的值.
为顶点的四边形是轴对称图形?直接写出h的值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②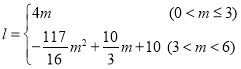 ;(3)h=3或
;(3)h=3或![]() 或
或![]() .
.
【解析】
试题分析:(1)把(0,0)代入![]() 即可解决问题.
即可解决问题.
(2)①用m的代数式表示PQ、QQ′,即可解决问题.
②分0<m≤3或3<m<6两种情形,画出图形,利用相似三角形或锐角三角函数求出相应线段即可解决.
(3),①当h=3时,两个抛物线对称轴x=3,四边形OAQQ′是等腰梯形.②当四边形OQ′1Q1A是菱形时,求出抛物线对称轴即可解决问题.
试题解析:(1)∵抛物线![]() 经过原点,∴x=0时,y=0,∴9a+4=0,∴
经过原点,∴x=0时,y=0,∴9a+4=0,∴![]() ;
;
(2)∵抛物线![]() 经过原点时,∴h=0,∵
经过原点时,∴h=0,∵![]() ,∴
,∴![]() .
.
①将![]() 化为
化为![]() ;设P(m,
;设P(m,![]() ),Q(m,
),Q(m,![]() ),∴PQ=
),∴PQ=![]() ,QQ′=2m,∴
,QQ′=2m,∴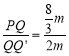 =
=![]() ;
;
②如图1中,当0<m≤3时,设PQ与OB交于点E,与OA交于点F,∵![]() ,∠PQQ′=∠BMO=90°,∴△PQQ′∽△BMO,∴∠QPQ′=∠OBM,∵EF∥BM,∴∠OEF=∠OBM,∴∠OEF=∠QPQ′,∴OE∥PQ′,∵
,∠PQQ′=∠BMO=90°,∴△PQQ′∽△BMO,∴∠QPQ′=∠OBM,∵EF∥BM,∴∠OEF=∠OBM,∴∠OEF=∠QPQ′,∴OE∥PQ′,∵![]() ,∴EF=
,∴EF=![]() ,OE=
,OE=![]() ,∴l=OF+EF+OE=
,∴l=OF+EF+OE=![]() =4m;
=4m;
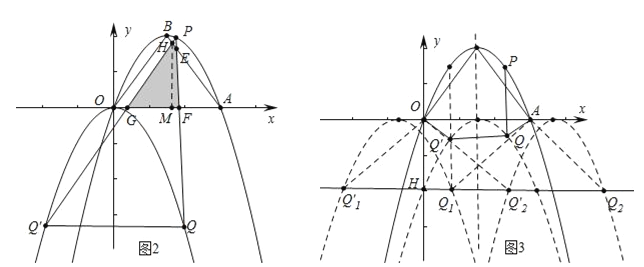
当3<m<6时,如图2中,设PQ′与AB交于点H,与x轴交于点G,PQ交AB于E,交OA于F,作HM⊥OA于M.
∵AF=6﹣m,tan∠EAF=![]() ,∴EF=
,∴EF=![]() ,AE=
,AE=![]() ,∵tan∠PGF=
,∵tan∠PGF=![]() ,PF=
,PF=![]() ,∴GF=
,∴GF=![]() ,∴AG=
,∴AG=![]() ,∴GM=AM=
,∴GM=AM=![]() ,∵HG=HA=
,∵HG=HA=![]() =
=![]() ,∴l=GH+EH+EF+FG=
,∴l=GH+EH+EF+FG=![]() .
.
综上所述: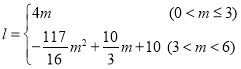 .
.
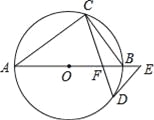
(3)如图3中,①当h=3时,两个抛物线对称轴x=3,∴点O、A关于对称轴对称,点Q,Q′关于对称轴对称,∴OA∥QQ′,OQ′=AQ,∴四边形OAQQ′是等腰梯形,属于轴对称图形.
②当四边形OQ′1Q1A是菱形时,OQ′1=OA=6,∵Q′1Q1=OA=6,∴点Q1的纵坐标为4,在RT△OHQ′1,中,OH=4,OQ′1=6,∴HQ′1=![]() ,∴h=
,∴h=![]() 或
或![]() ;
;
综上所述:h=3或![]() 或
或![]() 时,点O,A,Q,Q′为顶点的四边形是轴对称图形.
时,点O,A,Q,Q′为顶点的四边形是轴对称图形.