题目内容
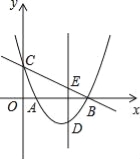
【题目】如图,抛物线y=x2﹣3x+![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
【答案】(1)y=-![]() x
x![]() ;(2)D点的坐标为(
;(2)D点的坐标为(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用坐标轴上点的特点求出A、B、C点的坐标,再用待定系数法求得直线BC的解析式;
(2)设点D的横坐标为m,则纵坐标为(m,![]() ),E点的坐标为(m,-
),E点的坐标为(m,-![]() m+
m+![]() ),可求得两点间的距离为d=﹣m2+
),可求得两点间的距离为d=﹣m2+![]() m,利用二次函数的最值即可求得m的值,也就求得了点D的坐标.
m,利用二次函数的最值即可求得m的值,也就求得了点D的坐标.
试题解析:(1)∵抛物线y=x2﹣3x+![]() 与x轴相交于A、B两点,与y轴相交于点C,
与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x=![]() 或x=
或x=![]() ,
,
∴A(![]() ,0),B(
,0),B(![]() ,0);
,0);
令x=0,则y=![]() ,
,
∴C点坐标为(0,![]() ),
),
设直线BC的解析式为:y=kx+b,则有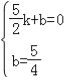 ,
,
解得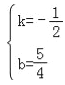 ,
,
∴直线BC的解析式为:y=-![]() x
x![]() ;
;
(2)设点D的横坐标为m,则纵坐标为(m,![]() ),
),
∴E点的坐标为(m,-![]() m+
m+![]() ),
),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d=—![]() m+
m+![]() ﹣(m2﹣3m+
﹣(m2﹣3m+![]() ),
),
整理得,d=﹣m2+![]() m,
m,
∵a=﹣1<0,
∴当m=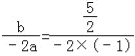 =
=![]() 时,d最大=
时,d最大=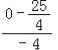 =
=![]() ,
,
∴D点的坐标为(![]() ,
,![]() ).
).

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目