题目内容
【题目】如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 . 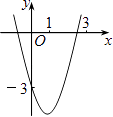
【答案】1(在﹣2<b<2范围内的任何一个数)
【解析】解:把(0,﹣3)代入抛物线的解析式得:c=﹣3,
∴y=x2+bx﹣3,
∵使该抛物线与x轴的一个交点在(1,0)和(3,0)之间,
∴把x=1代入y=x2+bx﹣3得:y=1+b﹣3<0
把x=3代入y=x2+bx﹣3得:y=9+3b﹣3>0,
∴﹣2<b<2,
即在﹣2<b<2范围内的任何一个数都符合,
所以答案是:1(在﹣2<b<2范围内的任何一个数).
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).

练习册系列答案
相关题目