题目内容
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
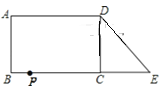
【答案】3或13
【解析】
由条件可知BP=t,当点P在线段BC上时可知BP=CE,当点P在线段DA上时,则有AD=CE,分别可得到关于t的方程,可求得t的值.
解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=3,根据SAS证得△ABP≌△DCE,
由题意得:BP=t=3,
所以t=3,
因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=3,根据SAS证得△BAP≌△DCE,
由题意得:AP=16-t=3,
解得t=13.
所以,当t的值为3或13秒时.△ABP和△DCE全等.
故答案为: 3或13.

练习册系列答案
相关题目
【题目】某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:

(1)根据上图求出下表所缺数据;
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 10 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.