题目内容
如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM= EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
(1)抛物线的解析式为y=x2﹣2x﹣8,顶点D的坐标为(1,﹣9);
(2)点P的坐标为(2,﹣8);
(3)要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
解析试题分析:(1)由于抛物线与x轴的两个交点已知,抛物线的解析式可设成交点式:y=a(x+2)(x﹣4),然后将点C的坐标代入就可求出抛物线的解析式,再将该解析式配成顶点式,即可得到顶点坐标.
(2)先求出直线CD的解析式,再求出点E的坐标,然后设点P的坐标为(m,n),从而可以用m的代数式表示出PM、EF,然后根据PM= EF建立方程,就可求出m,进而求出点P的坐标.
EF建立方程,就可求出m,进而求出点P的坐标.
(3)先求出点M的坐标,然后设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
试题解析:(1)根据题意可设抛物线的解析式为y=a(x+2)(x﹣4).
∵点C(0,﹣8)在抛物线y=a(x+2)(x﹣4)上,
∴﹣8a=﹣8.
∴a=1.
∴y=(x+2)(x﹣4)=x2﹣2x﹣8=(x﹣1)2﹣9.
∴抛物线的解析式为y=x2﹣2x﹣8,顶点D的坐标为(1,﹣9);
(2)如图,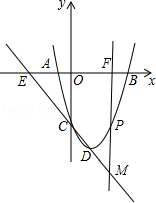
设直线CD的解析式为y=kx+ B.
∴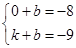
解得:  .
.
∴直线CD的解析式为y=﹣x﹣8.
当y=0时,﹣x﹣8=0,
则有x=﹣8.
∴点E的坐标为(﹣8,0).
设点P的坐标为(m,n),
则PM=(m2﹣2m﹣8)﹣(﹣m﹣8)=m2﹣m,EF=m﹣(﹣8)=m+8.
∵PM= EF,
EF,
∴m2﹣m= (m+8).
(m+8).
整理得:5m2﹣6m﹣8=0.
∴(5m+4)(m﹣2)=0
解得:m1=﹣ ,m2=2.
,m2=2.
∵点P在对称轴x=1的右边,
∴m=2.
此时,n=22﹣2×2﹣8=﹣8.
∴点P的坐标为(2,﹣8);
(3)当m=2时,y=﹣2﹣8=﹣10.
∴点M的坐标为(2,﹣10).
设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,
①若抛物线y=x2﹣2x﹣8+c与直线y=﹣x﹣8相切,
则方程x2﹣2x﹣8+c=﹣x﹣8即x2﹣x+c=0有两个相等的实数根.
∴(﹣1)2﹣4×1×c=0.
∴c= .
.
②若抛物线y=x2﹣2x﹣8+c经过点M,
则有22﹣2×2﹣8+c=﹣10.
∴c=﹣2.
③若抛物线y=x2﹣2x﹣8+c经过点E,
则有(﹣8)2﹣2×(﹣8)﹣8+c=0.
∴c=﹣72.
综上所述:要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
考点:二次函数综合题.

某商品现在的售价为每件35元.每天可卖出50件.市场调查反映:如果调整价格.每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?
设每件商品降价x元.每天的销售额为y元.
(1)分析:根据问题中的数量关系.用含x的式子填表:
| | 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 |
| 每件售价(元) | 35 | 34 | 33 | … | |
| 每天售量(件) | 50 | 52 | 54 | … | |
(2)(由以上分析,用含x的式子表示y,并求出问题的解)
 ,当1≤x≤4,
,当1≤x≤4,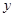 的取值范围为 .
的取值范围为 .

 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.

 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点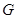 .
. 的坐标分别是
的坐标分别是 的抛物线的解析式;
的抛物线的解析式; ,顶点为点
,顶点为点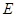 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.