题目内容
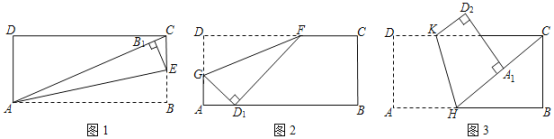
【题目】如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为______.

【答案】4![]()
【解析】分析:利用点的对称,让△AMN的三边在同一直线上,即作出A关于BC和ED的对称点A′,A″,即可得出最短路线,再利用勾股定理,求出即可.
详解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.
过A′作EA延长线的垂线,垂足为H,

∵AB=BC=2,AE=DE=4,
∴AA′=2BA=4,AA″=2AE=8,
则Rt△A′HA中,
∵∠EAB=120°,
∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH=![]() AA′=2,
AA′=2,
∴A′H=![]() ,,
,,
A″H=2+8=10,
∴A′A″=![]() .
.
故答案为:![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
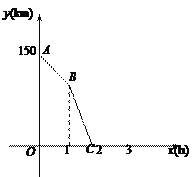
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.