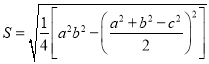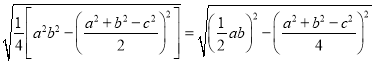��Ŀ����
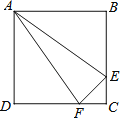
����Ŀ����ƽ��ֱ������ϵ�У�����ֱ�����ǰ�����ҵ�һԪ���η��̵�ʵ������������ڷ���x2��5x+2��0�����������ǣ���һ�������ݷ���ϵ��������ȷ��һ�Թ̶���A��0��1����B��5��2�����ڶ�����������ƽ�����ƶ�һ��ֱ�����ǰ壬ʹһ��ֱ�DZߺ����A����һ��ֱ�DZߺ����B�������������ƶ������У������ǰ��ֱ�Ƕ�������x���ϵ�C��ʱ����C�ĺ�����m��Ϊ�÷��̵�һ��ʵ��������ͼ1�������IJ����������ǰ�ֱ�Ƕ����λ�ã���������x������һ��D��ʱ����D�ĺ�����Ϊn��Ϊ�÷��̵���һ��ʵ��������1����ͼ2�У����ա����IJ����IJ�������������D���뱣��������Dʱֱ�����ǰ�����ֱ�DZߵĺۼ�������2�����ͼ1����֤�����������������õ���m���Ƿ���x2��5x+2��0��һ��ʵ������
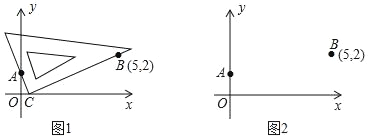
���𰸡���1������������2����������
��������
��1��������������ͼ�μ��ɣ�
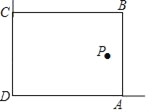
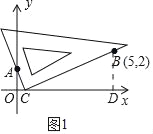
��2����ͼ1�У���BD��x����D���������������ε����ʼ��ɽ�����⣮
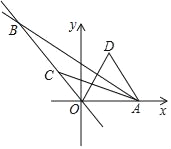
�⣺��1����D��ͼ��ʾ��
��2����ͼ1�У���BD��x����D��
�ߡ�AOC����ACB����CDB��90����
���ACO+��BCD��90������BCD+��CBD��90����
���ACO����CBD��
���ACO�ס�CBD��
��![]()
��![]()
�����ã�m2��5m+2��0��
��m�Ƿ���x2��5x+2��0��ʵ������

 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�