题目内容
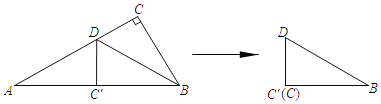
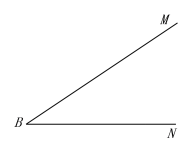
【题目】(1)如图，已知线段
和
，请在给出的图形上用尺规作出
,使得：点
在射线
上，点
在射线
上，且
，
；(保留作图痕迹，不写作法)
(2)求证：直角三角形斜边上的中线等于斜边的一半.(要求：利用（1）中的Rt,画出斜边
上的中线
，写出已知、求证和证明过程)
【答案】（1）如图
为所作图形；见解析；（2）见解析.
【解析】
（1）根据题目作图要求进行作图即可；
（2）先根据题意画出图形，再证明．延长CD至E使CD=DE，连接AE、BE，因为D是AB的中点，所以AD=BD，因为CD=DE，所以四边形ACBE是平行四边形，因为∠ACB=90°，所以四边形ACBE是矩形，根据矩形的性质可得出结论．
（1）如图为所作图形；
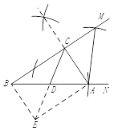
（2）已知：如图，
为Rt中斜边
上的中线，
，
求证：
.
证明：延长并截取
.
∵为边中线，∴
，
∴四边形
为平行四边形.
∵，
∴□为矩形，
∴
，
∴
练习册系列答案
相关题目
【题目】我市“木兰溪左岸绿道”工程已全部建成并投入使用，10公里的河堤便道铺满了彩色的透水沥青，堤岸旁的各类花草争奇斗艳，与木兰溪河滩上的特色花草相映成趣，吸引着众多市民在此休闲锻炼、散步观光．某小区随机调查了部分居民在一周内前往“木兰溪左岸绿道”锻炼的次数，并制成如图不完整的统计图表：
居民前往“木兰溪左岸绿道”锻炼的次数统计表
锻炼次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息，解答下列问题：
（1）a＝ ，b＝ ．
（2）请计算扇形统计图中“3次”所对应扇形的圆心角的度数；
（3）若该小区共有2000名居民，根据调查结果，估计该小区居民在一周内前往木兰溪左岸绿道”锻炼“4次及以上”的人数．
