题目内容
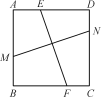
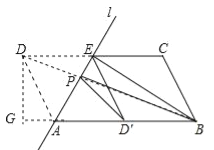
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论;(2)由四边形DAD′E是平行四边形,得到DAD′E是菱形,推出D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,解直角三角形得到AG=![]() ,DG=
,DG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴CE=D′B,CE∥D′B,
∴四边形BCED′是平行四边形;
∵AD=AD′,
∴DAD′E是菱形,
(2)∵四边形DAD′E是菱形,
∴D与D′关于AE对称,
连接BD交AE于P,则BD的长即为PD′+PB的最小值,
过D作DG⊥BA于G,
∵CD∥AB,
∴∠DAG=∠CDA=60°,
∵AD=1,
∴AG=![]() ,DG=
,DG=![]() ,
,
∴BG=![]() ,
,
∴BD=![]() =
=![]() ,
,
∴PD′+PB的最小值为![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案