题目内容
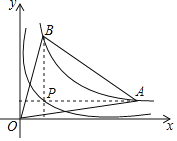
【题目】如图，在平面直角坐标系中，正比例函数y=kx的图象与反比例函数y=
的图象经过点A（2，2）．
（1）分别求这两个函数的表达式；
（2）将直线OA向上平移3个单位长度后与y轴交于点B，与反比例函数图象在第一象限内的交点为C，连接AB，AC，求点C的坐标及△ABC的面积；
（3）在第一象限内，直接写出反比例函数的值大于直线BC的值时，自变量x的取值范围．
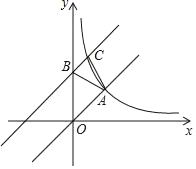
【答案】（1）y=x，y=
；（2）C（1，4）；
；（3）0＜x＜1.
【解析】分析：（1）将点A（2，2）代入正比例函数中即可求出k的值，再将A（2，2）代入反比例函数中即可求出m的值．
（2）由题意可知点B的坐标为（0，3），所以直线BC的解析式为y=x+3，联立直线BC的解析式与反比例函数的解析式即可求出C的坐标，连接OC，由于OA∥BC，所以△ABC的面积等于△BOC的面积．
（3）因为点C的坐标已知，在第一现象内，从图象直接观察可知x的取值范围．
详解：（1）将A（2，2）代入y=kx，
∴2k=2，
∴k=1，
∴正比例函数的解析式为：y=x
将A（2，2）代入y=
∴m=2×2=4，
∴反比例函数的解析式为：y=；
（2）∵直线BC由直线OA向上平移3个单位所得，
∴B（0，3）
∴直线BC的解析式为：y=x+3，
联立解得：
或
，
∵点C在第一象限，
∴点C的坐标为（1，4）
∵OA∥BC，
∴S△ABC=S△BOC=×3×1=，
（3）在第一象限内，要使反比例函数y=的值大于直线BCy=x+3的值，从图象可知
∵点C的坐标为（1，4）
∴0＜x＜1
【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表（近期两种材质的围棋的售价一直不变）：
塑料围棋 | 玻璃围棋 | 总价（元） | |
第一次（盒） |
|
|
|
第二次（盒） |
|
|
|
（1）若该社团计划再采购这两种材质的围棋各
盒，则需要多少元；
（2）若该社团准备购买这两种材质的围棋共
盒，且要求塑料围棋的数量不多于玻璃围棋数量的
倍，请设计出最省钱的购买方案，并说明理由．
