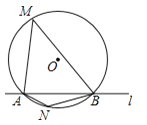Question

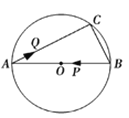
【题目】如图，AB是⊙O的直径，弦BC=6cm，AC=8cm．若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为___________．

Answer 1

【答案】，

【解析】

应分两种情况进行讨论：①当PQ⊥AC时，△APQ为直角三角形，根据△APQ∽△ABC，可将时间t求出；②当PQ⊥AB时，△APQ为直角三角形，根据△APQ∽△ACB，可将时间t求出．

解：∵AB是直径，
∴∠C=90°，
又∵BC=6cm，AC=8
∴AB=10，
则AP=（10-2t）cm，AQ=t，
∵当点P到达点A时，点Q也随之停止运动，
∴0＜t≤5，
①如图1，当PQ⊥AC时，PQ∥BC，则
△APQ∽△ABC，
∴，
∴，
解得t=，
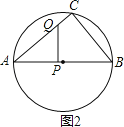
②如图2，当PQ⊥AB时，△APQ∽△ACB，
则，解得

故答案为：，．