题目内容
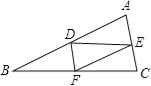
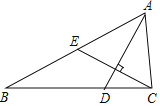
【题目】已知：如图，AD、CE分别是△ABC的角平分线和中线，AD⊥CE，AD＝CE＝4，则BC的长等于_____．
【答案】
【解析】
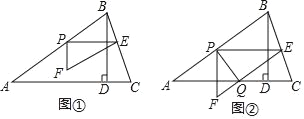
如下图，过点B作CE的垂线，交CE延长线于点F，先证△BFE≌△AHE，然后利用AD⊥CE可得FE、EH、HC的长，接着证△BFE∽△DHC，利用线段比的关系可求得BC的长．
如下图，过点B作CE的垂线，交CE延长线于点F，AD与CE交于点H．
∵AD⊥EC，AD是∠EAC的角平分线
∴∠EAH=∠HAC
∴∠AEH=∠ACH，∴AE=AC，△AEC是等腰三角形
∵CE=4
∴EH=HC=2
∵CE是△ABC的中线，∴AE=EB
∵∠AEH=∠FEB，∠AHE=∠BFE=90°
∴△AEH≌△BEF
∴EF=2，FC=2+2+2=6，BF=AH
∵∠DCH=∠BCF，∠DHC=∠BFC=90°
∴△DCH∽△BCF
∴
∴3DH=BF，∴3DH=HA
∵AD=4
∴HD=1，FB=3
∴在Rt△CBF中，CB=
故答案为：
练习册系列答案
相关题目
