Question

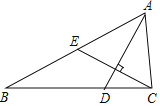
【题目】如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形共有多少个？( )

A.12B.16C.24D.25

Answer 1

【答案】D

【解析】

如下图，先对网格进行编号，然后找出所有符合条件的平行四边形即可．

如下图，对网格编号

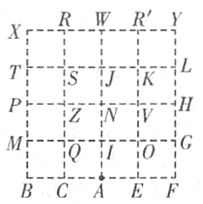
情况一：平行四边形的一个点在BF上，另两个点在MG上，有：

ABMI、ABQO、ABIG、AFGI、AFOQ、AFIM共6个

情况二：平行四边形的一个点在BF上，另两个点在PH上，有：

AEHV、AEVN、AENZ、AEZP、ACPZ、ACZN、ACNV、ACVH共8个

情况三：其他符合条件平行四边形有：

AQNO、AIYL、ATXI、AHLI、APTI、AGHI、AMPI、AZRN、AVN、AOKN、AQSN共11种

故共有：6+8+11=25种

故答案为：25