题目内容
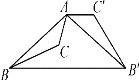
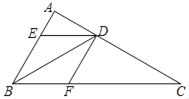
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.
【答案】(1)证明见解析;(2)S四边形BEDF=6![]() .
.
【解析】
(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;
(2)过点D作DH⊥BC于点H,由题意可得BD=CD=6,根据30度所对的直角边等于斜边的一半,可求DH=3,即可求DF=BF的长,即可得菱形BEDF的面积.
(1)∵DE∥BC,DF∥AB,∴四边形DEBF是平行四边形.
∵DE∥BC,∴∠EDB=∠DBF.
∵BD平分∠ABC,∴∠ABD=∠DBF![]() ∠ABC,∴∠ABD=∠EDB,∴DE=BE且四边形BEDF为平行四边形,∴四边形BEDF为菱形.
∠ABC,∴∠ABD=∠EDB,∴DE=BE且四边形BEDF为平行四边形,∴四边形BEDF为菱形.
(2)如图:过点D作DH⊥BC于点H.
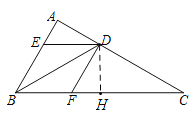
∵∠A=90°,∠C=30°,∴∠ABC=60°,∴∠DBC=30°=∠C,∴DB=DC=6.
∵DH⊥BC,∠C=30°,∴DC=2DH=6,∴DH=3.
∵DF∥AB,∴∠A=∠FDC=90°,且∠C=30°,DC=6,∴DC![]() DF,∴DF=2
DF,∴DF=2![]() .
.
∵四边形BEDF为菱形,∴BF=DF=2![]() ,∴S四边形BEDF=BF×DH=2
,∴S四边形BEDF=BF×DH=2![]() 3=6
3=6![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
刹车时车速/km·h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?