题目内容
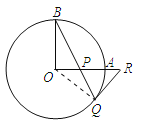
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OQ,由QR为圆O的切线,得到∠OQR为90°,即∠OQB+∠PQR=90°,由OA与OB垂直,根据垂直的定义得到∠BOA=90°,所以∠B+∠BPO=90°,再根据对顶角相等及等角的余角相等,得到∠RPQ=∠RQP,根据“等角对等边”得证;
(2)根据OP=PQ,由“等边对等角”得到∠POQ=∠PQO,又根据半径OB=OQ,再根据“等边对等角”得到∠B=∠BQO,在三角形OBQ中,由∠BOA为直角,设出∠B=∠PQO=∠POQ=x,根据三角形的内角和定理列出关于x的方程,求出方程的解得到x的值,即为∠B的度数,又∠RPQ=∠BPO=60°,PR=QR,所以三角形PRQ为等边三角形,所以PQ=QR,在直角三角形OQR中,根据30°的正切函数定义,由OQ=OB=2,即可求出QR的值,从而得到PQ的长.
(1)连接OQ.∵QR是切线,∴∠OQR=90°,∴∠BQO+∠PQR=90°.
∵OA⊥OB,∴∠BOA=90°,∴∠B+∠BPO=90°,又∠BPO=∠RPQ,∴∠B+∠RPQ=90°.
由OB=OQ得:∠B=∠BQO,∴∠RPQ=∠RQP,∴PR=QR;
(2)∵OP=PQ,∴∠POQ=∠PQO,
又OB=OQ,∴∠B=∠PQO,
设∠B=∠PQO=∠POQ=x,又∠BOP=90°,
根据三角形内角和定理得:
∠B+∠BOP+∠POQ+∠PQO=180°,即x+90°+x+x=180°,
解得:x=30°,即∠B=30°,∴∠RPQ=∠BPO=60°,又PR=QR,∴△PQR为等边三角形,即PQ=QR=PR,
在直角三角形OQR中,OQ=OB=2,
根据锐角三角函数定义得:
![]() .
.