题目内容
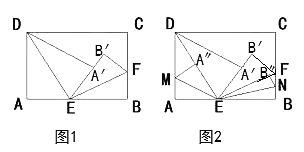
【题目】如图1,长方形ABCD沿着直线DE和EF折叠,使得AB的对应点![]() 和点E在同一条直线上。
和点E在同一条直线上。
(1)求∠DEF的度数;
(2)如图2,若再次沿着直线EM和EN折叠使得A、B的对应点![]() 分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
【答案】(1)90°;(2)11°.
【解析】
(1)根据折叠的性质得到∠AED=∠A′ED,∠BEF=∠B′EF,再根据平角的定义得到∠AED+∠A′ED+∠BEF+∠B′EF=180°,即可得到∠FED的度数;
(2)由(1)得∠AED+∠BEF=180°-∠FED=180°-90°=90°,根据折叠的性质得到∠AEM=∠![]() EM,∠BEN=∠
EM,∠BEN=∠![]() EN,所以∠AEM+∠BEN=
EN,所以∠AEM+∠BEN=![]() (∠AED+∠BEF)=
(∠AED+∠BEF)=![]() ×90°=45°,可得∠BEN=45°-∠AEM.
×90°=45°,可得∠BEN=45°-∠AEM.
解:(1)因为长方形纸片的一角折叠,顶点A落在A′处,另一角折叠,顶点B落在EA′上的B′点处,
所以∠AED=∠A′ED,∠BEF=∠B′EF,而∠AED+∠A′ED+∠BEF+∠B′EF=180°
所以∠A′ED+∠B′EF=90°,即∠FED=90°.
(2)因为由(1)得∠AED+∠BEF=180°-∠FED=180°-90°=90°,根据折叠的性质得到∠AEM=∠![]() EM,∠BEN=∠
EM,∠BEN=∠![]() EN,所以∠AEM+∠BEN=
EN,所以∠AEM+∠BEN=![]() (∠AED+∠BEF)=
(∠AED+∠BEF)=![]() ×90°=45°,因为∠AEM=34°,所以∠BEN=45°-∠AEM=45°-34°=11°.
×90°=45°,因为∠AEM=34°,所以∠BEN=45°-∠AEM=45°-34°=11°.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目