题目内容
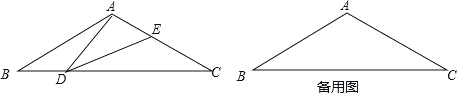
【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
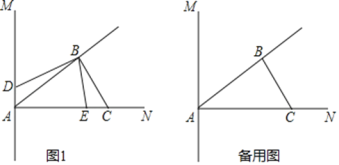
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
【答案】(1)当t=![]() s或4s时,满足S△ADB:S△BEC=2:1;(2)t的值为2s或6s
s或4s时,满足S△ADB:S△BEC=2:1;(2)t的值为2s或6s
【解析】
(1)作BH⊥AC于H,BG⊥AM于G.由BA平分∠MAN,推出BG=BH,由S△ADB:S△BEC=2:1,AD=t,AE=2t,可得![]() tBG:
tBG:![]() (6-2t)BH=2:1,解方程即可解决问题;
(6-2t)BH=2:1,解方程即可解决问题;
(2)存在.由BA=BC,∠BAD=∠BCE=45°,可知当AD=EC时,△ADB≌△CEB,列出方程即可解决问题.
解:(1)如图2中,
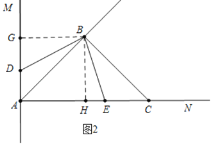
①当E在线段AC上时,作BH⊥AC于H,BG⊥AM于G.
∵BA平分∠MAN,
∴BG=BH,
∵S△ADB:S△BEC=2:1,AD=t,AE=2t,
∴![]() tBG :
tBG :![]() (6﹣2t)BH=2:1,
(6﹣2t)BH=2:1,
∴t=![]() s.
s.
②当点E运动到AC延长线上,同法可得t=4时,也满足条件,
∴当t=![]() s或4s时,满足S△ADB:S△BEC=2:1.
s或4s时,满足S△ADB:S△BEC=2:1.
(2)存在.当D在AM延长线上时
∵BA=BC,∠BAD=∠BCE=45°,
∴当AD=EC时,△ADB≌△CEB,
∴t=6﹣2t,
∴t=2s,
∴t=2s时,△ADB≌△CEB.
当D在MA延长线上时,2t﹣6=t,t=6s,
综上所述,满足条件的t的值为2s或6s

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案