题目内容
【题目】如图,将边长为 ![]() 的正方形
的正方形 ![]() 的一边
的一边 ![]() 与直角边分别是
与直角边分别是 ![]() 和
和 ![]() 的
的 ![]() 的一边
的一边 ![]() 重合.正方形
重合.正方形 ![]() 以每秒
以每秒 ![]() 个单位长度的速度沿
个单位长度的速度沿 ![]() 向右匀速运动,当点
向右匀速运动,当点 ![]() 和点
和点 ![]() 重合时正方形停止运动.设正方形的运动时间为
重合时正方形停止运动.设正方形的运动时间为 ![]() 秒,正方形
秒,正方形 ![]() 与
与 ![]() 重叠部分面积为S,则S关于
重叠部分面积为S,则S关于 ![]() 的函数图象为( )
的函数图象为( )
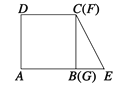
A. 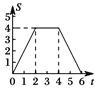 B.
B. 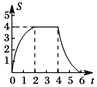 C.
C.  D.
D. 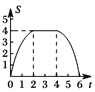
【答案】B
【解析】
分类讨论:当0≤t≤2时,BG=t,BE=2-t,运用△EBP∽△EGF的相似比可表示PB=4-2t,S为梯形PBGF的面积,则S=![]() (4-2t+4)t=-t2+4t,其图象为开口向下的抛物线的一部分;
(4-2t+4)t=-t2+4t,其图象为开口向下的抛物线的一部分;
当2<t≤4时,S=![]() FGGE=4,其图象为平行于x轴的一条线段;
FGGE=4,其图象为平行于x轴的一条线段;
当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),所以S为三角形PAE的面积,则S=(t-6)2,其图象为开口向上的抛物线的一部分.
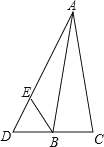
当0≤t≤2时,如图
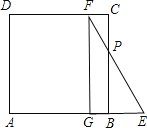 ,
,
BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴![]() ,即
,即![]() ,
,
∴PB=4-2t,
∴S=![]() (PB+FG)GB=
(PB+FG)GB=![]() (4-2t+4)t=-t2+4t;
(4-2t+4)t=-t2+4t;
当2<t≤4时,S=![]() FGGE=4;
FGGE=4;
当4<t≤6时,如图,
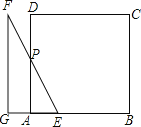
GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴![]() ,即
,即![]() ,
,
∴PA=2(6-t),
∴S=![]() PAAE=
PAAE=![]() ×2×(6-t)(6-t)
×2×(6-t)(6-t)
=(t-6)2,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选:B.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】下表是随机抽取的某公司部分员工的月收入资料.
月收入/元 | 45000 | 18000 | 10000 | 5500 | 5000 | 3400 | 3000 | 2000 |
人数 | 1 | 1 | 1 | 3 | 6 | 1 | 11 | 2 |
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
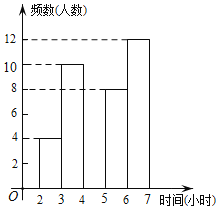
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?