题目内容
【题目】结论:直角三角形中,![]() 的锐角所对的直角边等于斜边的一半.
的锐角所对的直角边等于斜边的一半.
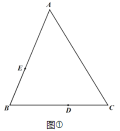
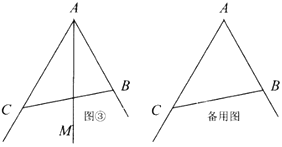
如图①,我们用几何语言表示如下:
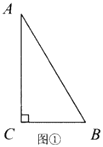
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
你可以利用以上这一结论解决以下问题:
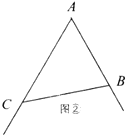
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 的面积;
的面积;
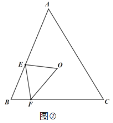
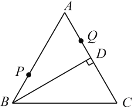
(2)如图③,射线![]() 平分
平分![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着射线
出发,以每秒1个单位的速度沿着射线![]() 的方向运动,过点
的方向运动,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)过点C作CH⊥AB于点H,则∠CAH=90°,即可求出∠ACH=30°,求出AH,根据勾股定理即可求解;
(2)分两种情况讨论①当点P在△ABC内部时②当点P在△ABC外部时,连结PB、PC,利用面积法进行求解即可.
(1)过点C作CH⊥AB于点H,则∠CAH=90°,如图②
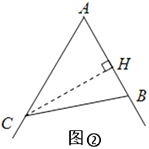
∵![]()
∴∠ACH=30°
∴![]()
∴![]()
∴![]()
(2)分两种情况讨论
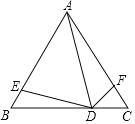
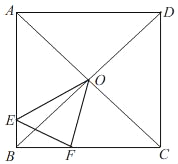
①当点P在△ABC内部时,如图③所示,连结PB、PC.
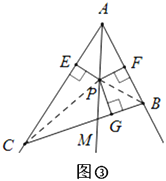
设PE=PF=PG=x
∵![]()
∴![]()
∴![]()
∵AM平分∠BAC,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
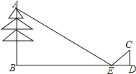
②当点P在△ABC外部时,如图④所示,连结PB、PC.
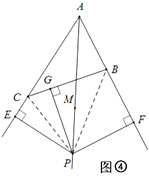
设PE=PF=PG=x,
∵![]()
∴![]() ,
,
解得![]()
![]()
由①知,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]()
![]()
∴![]()
![]()
∴当PE=PF=PG时,
![]() 或
或![]()

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目