题目内容
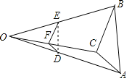
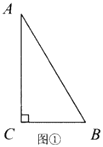
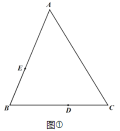
【题目】已知△![]() .
.
(1)在图中用直尺和圆规作出![]() 的平分线和
的平分线和![]() 边的垂直平分线交于点
边的垂直平分线交于点![]() (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法).
(2)在(1)的条件下,若点![]() 、
、![]() 分别是边
分别是边![]() 和
和![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 求证:
求证:![]() ;
;
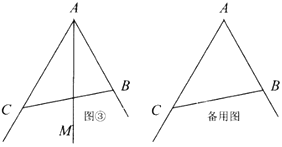
(3)如图,在(1)的条件下,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且△
边上的点,且△![]() 的周长等于
的周长等于![]() 边的长,试探究
边的长,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)见解析;(2)见解析;(3)![]() 与
与![]() 的数量关系是
的数量关系是![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用基本作图作∠ABC的平分线;利用基本作图作BC的垂直平分线,即可完成;
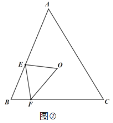
(2)如图,设BC的垂直平分线交BC于G,作OH⊥AB于H,
用角平分线的性质证明OH=OG,BH=BG,继而证明EH =DG,然后可证明![]() ,于是可得到OE=OD;
,于是可得到OE=OD;
(3)作OH⊥AB于H,OG⊥CB于G,在CB上取CD=BE,利用(2)得到 CD=BE,![]() ,OE=OD,
,OE=OD,![]() ,
,![]() ,可证明
,可证明![]() ,故有
,故有![]() ,由△
,由△![]() 的周长=BC可得到DF=EF,于是可证明
的周长=BC可得到DF=EF,于是可证明![]() ,所以有
,所以有![]() ,然后可得到
,然后可得到![]() 与
与![]() 的数量关系.
的数量关系.
解:(1)如图,就是所要求作的图形;
(2)如图,设BC的垂直平分线交BC于G,作OH⊥AB于H,
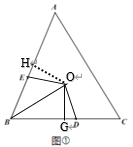
∵BO平分∠ABC,OH⊥AB,OG垂直平分BC,
∴OH=OG,CG=BG,
∵OB=OB,
∴![]() ,
,
∴BH=BG,
∵BE=CD,
∴EH=BH-BE=BG-CD=CG-CD=DG,
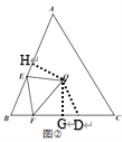
在![]() 和
和![]() 中,
中,
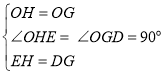 ,
,
∴![]() ,
,
∴OE=OD.
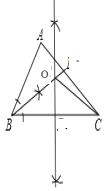
(3)![]() 与
与![]() 的数量关系是
的数量关系是![]() ,理由如下;
,理由如下;
如图,作OH⊥AB于H,OG⊥CB于G,在CB上取CD=BE,
由(2)可知,因为 CD=BE,所以![]() 且OE=OD,
且OE=OD,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵△![]() 的周长=BE+BF+EF=CD+BF+EF=BC
的周长=BE+BF+EF=CD+BF+EF=BC
∴DF=EF,
在△![]() 和△
和△![]() 中,
中,
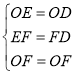 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示:
批发价(元个) | 零售价(元/个) | |
甲型号垃圾桶 | 12 | 16 |
乙型号垃圾桶 | 30 | 36 |
若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,
(1)求y关于x的函数表达式.
(2)若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).