��Ŀ����
��ͼ�٣�һ����ֱ�Ĺ�·����A��B��C���أ�B��C�������150ǧ�ף��ס������������ֱ��B��C����ͬʱ�������ع�·����������У��ֱ�ʻ��C��B���أ��ס���������A�صľ���y1��y2��ǧ�ף�����ʻʱ��x��ʱ���Ĺ�ϵ��ͼ����ʾ������ͼ���������̽����

��1������ͼ���б��A�ص�λ�ã�������Ҫ������˵����
��2����ͼ����M������꣬�����õ��ʵ�����壻
��3����ͼ���в�ȫ�׳��ĺ���ͼ����׳���A�صľ���y1����ʻʱ��x�ĺ�����ϵʽ��
��4��A������ָ�����ģ�ָ�����ļ����������жԽ����������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ��������������ͬʱ��ָ�������öԽ���ͨ����ʱ�䣮
��1��A��λ�ü�ͼ�Σ�ʹ��A����AB��AC=2��3��
��2����M��ʾ�ҳ�1.2Сʱ����A�أ�
��3��ͼ�����������0��x��1ʱ��y1=��60x+60�� ��1��x��2.5ʱ��y1=60x��60��
��4����������ͬʱ��ָ�������öԽ�����ʱ��Ϊ Сʱ��
Сʱ��
���������������1����ͼ�����ͼʾ������֪��A����AB��AC=2��3��
��2��ֱ�Ӹ���������ʽ�����ҳ����ٶ�150��2=75ǧ��/ʱ��90��75=1.2�����Ե�M��ʾ�ҳ�1.2Сʱ����A�أ�
��3������ͼ���֪��0��x��1ʱ��y1=��60x+60����1��x��2.5ʱ��y1=60x��60��
��4�����ݡ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ������Ϊ���ȹ�ϵ�в���ʽ�飬��⼴�ɵõ�ͨ����ʱ�䷶Χ�����Կ�������ͬʱ��ָ������ͨ����ʱ��Ϊ Сʱ��
Сʱ��
�����������1��A��λ����ͼ��ʾ��ʹ��A����AB��AC=2��3��
��2���ҳ����ٶ�150��2=75ǧ��/ʱ��90��75=1.2����M��1.2��0����
���Ե�M��ʾ�ҳ�1.2Сʱ����A�أ�
��3���׳��ĺ���ͼ����ͼ��ʾ�� 
��0��x��1ʱ��y1=��60x+60��
��1��x��2.5ʱ��y1=60x��60��
��4���������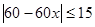 �����
����� ��
�� �����
����� ��
��
����������ͬʱ��ָ�������öԽ�����ʱ��Ϊ Сʱ��
Сʱ��
���㣺һ�κ�����Ӧ�ã�

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д��ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
| ʱ��x���죩 | 1��x��50 | 50��x��90 |
| �ۼۣ�Ԫ/���� | x��40 | 90 |
| ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ[
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�����.
�����ܻ�������̼��������dz�����һ�����ʽ��ij�ҵ��̳��ƻ���11.8��Ԫ���������͵��ӻ���ϴ�»��Ϳյ���40̨�����ּҵ�Ľ��ۺ��ۼ������ʾ��
| �۸����� | ���ۣ�Ԫ/̨�� | �ۼۣ�Ԫ/̨�� |
| ���ӻ� | 5000 | 5500 |
| ϴ�»� | 2000 | 2160 |
| �յ� | 2400 | 2700 |
��2���ڡ�2012�����Ѵٽ��¡�������ڼ䣬�̼���������ֽ����Ͳ�Ʒ�Ƴ����ֽ�ÿ��1000Ԫ��50Ԫ�ҵ�����ȯһ�š�������͡��Ļ.�ڣ�1���������£������ֵ����ڻ�ڼ�ȫ���۳����̼�Ԥ������ͳ������ţ�
 ��x�ᡢy��ֱ��ڵ�A��B����C���߶�AB�ϣ���
��x�ᡢy��ֱ��ڵ�A��B����C���߶�AB�ϣ��� ��
�� ��ʱ����������ߵı���ʽ��
��ʱ����������ߵı���ʽ��
 (m��0)��ͼ���й�����A(1��2),D(a,-1)��ֱ�� ���ڵ�N(3��0)����һ�κ����ͷ����� ������ͼ��ֱ��ڵ�B��C��
(m��0)��ͼ���й�����A(1��2),D(a,-1)��ֱ�� ���ڵ�N(3��0)����һ�κ����ͷ����� ������ͼ��ֱ��ڵ�B��C��

 ��
�� Ϊ��ֵʱ������ͼ��ԭ�㣻
Ϊ��ֵʱ������ͼ��ԭ�㣻 ��.
��. ����һ����Ʒ
����һ����Ʒ
 ������ʱ��Ĺ�ϵʽ��
������ʱ��Ĺ�ϵʽ��