题目内容
如图,一次函数y=kx+b(k≠ 0)与反比例函数 (m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.
(1) 求一次函数与反比例函数的解析式;
(2) 求△ABC的面积。
(3) 根据图象回答,在什么范围时,一次函数的值大于反比例函数的值。
(1)y=x+1, ;(2)
;(2) ;(3)-2<x<0或x>.
;(3)-2<x<0或x>.
解析试题分析:(1)分别把A点坐标代入一次函数和反比例函数解析式求出k和m即可;
(2)利用直线l⊥x轴于点N(3,0)得到B、C点的横坐标,再利用(1)中的解析式可确定B与C点的纵坐标,然后利用三角形面积公式计算;
(3)先解方程组 确定一次函数与反比例函数的另一个交点为(-2,-1),然后观察函数图象得到当-2<x<0或x>1时,y1>y2.
确定一次函数与反比例函数的另一个交点为(-2,-1),然后观察函数图象得到当-2<x<0或x>1时,y1>y2.
试题解析:(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为 ;
;
(2)作AE⊥x轴于E,如图,
设一次函数与x轴交于D点,令y=0,求出x=-1,
∴D点坐标为(-1,0),
∵A(1,2),
∴AE=2,OE=1,
将x=3代入一次函数y=x+1得y=4,
将x=3代入反比例 ,
,
得
∴B(3,4),C(3, ),
),
∴S△ABC= ×(3-1)×(4-
×(3-1)×(4- )=
)= ;
;
(3)解方程组 得
得 或
或 ,
,
∴一次函数与反比例函数的另一个交点为(-2,-1),
∴当-2<x<0或x>1时,y1>y2.
考点: 反比例函数与一次函数的交点问题.

练习册系列答案
相关题目
 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式:
 、线段
、线段 分别表示甲、乙两车所行路程
分别表示甲、乙两车所行路程 (千米)与时间
(千米)与时间 (小时)之间的函数关系对应的图象(线段
(小时)之间的函数关系对应的图象(线段 表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
 (k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(k1>0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2.



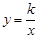 的图象的一个交点为A(1,m).
的图象的一个交点为A(1,m).
 的解析式;
的解析式; 的坐标(不写求解过程).
的坐标(不写求解过程). 的图象
的图象 是第一、三象限的角平分线.
是第一、三象限的角平分线.
 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线 、
、 的位置,并写出它们的坐标:
的位置,并写出它们的坐标:  的坐标为 .
的坐标为 . 的图象与反比例函数
的图象与反比例函数 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).