题目内容
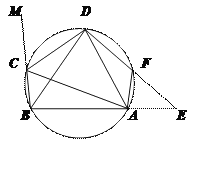
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 、
、![]() 是圆上的两点,且
是圆上的两点,且![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 延长线的垂线
延长线的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() 的半径为
的半径为![]() ,
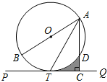
,![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.
【答案】![]()
【解析】
连接OT、OD、过O作OM⊥AD于M,得到矩形OMCT,求出OM,求出∠OAM,求出∠AOT,求出OT∥AC,得出PC是圆的切线,得出等边三角形AOD,求出∠AOD,求出∠DOT,求出∠DTC=∠CAT=30°,求出DC,求出梯形OTCD的面积和扇形OTD的面积.相减即可求出答案.
解:连接OT、OD、DT,过O作OM⊥AD于M,

∵OA=OT,AT平分∠BAC,
∴∠OTA=∠OAT,∠BAT=∠CAT,
∴∠OTA=∠CAT,
∴OT∥AC,
∵PC⊥AC,
∴OT⊥PC,
∵OT为半径,
∴PC是⊙O的切线,
∵OM⊥AC,AC⊥PC,OT⊥PC,
∴∠OMC=∠MCT=∠OTC=90°,
∴四边形OMCT是矩形,
∴OM=TC=![]() ,
,
∵OA=2,
∴sin∠OAM=![]() ,
,
∴∠OAM=60°,
∴∠AOM=30°
∵AC∥OT,
∴∠AOT=180°-∠OAM=120°,
∵∠OAM=60°,OA=OD,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠TOD=120°-60°=60°,
∵PC切⊙O于T,
∴∠DTC=∠CAT=![]() ∠BAC=30°,
∠BAC=30°,
∴tan30°=![]() =
=![]() ,
,
∴DC=1,
∴阴影部分的面积是S梯形OTCD-S扇形OTD=![]() ×(2+1)×
×(2+1)×![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目