Question

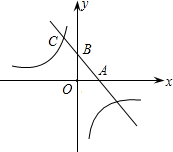如图，已知反比例函数y=

k

x

的图象经过点C（-3，8），一次函数的图象过点C且与x轴、y轴分别交于点A、B，若OA=3，且AB=BC．
（1）求反比例函数的解析式；（2）求AC和OB的长．

Answer 1

分析：（1）根据题意，反比例函数y=

k

x

的图象经过点C（-3，8），代入数据，解可得k的值，进而可得答案，
（2）过点C作CE⊥x轴，垂足为E，可得AE的长，进而可得AC的长，又AB=BC，OE=OA，故可得OB的长．

解答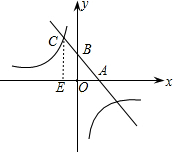：解：（1）依题意得：8=

k

-3

（2分）
∴k=-24．（3分）
∴反比例函数的解析式y=

-24

x

． （4分）

（2）过点C作CE⊥x轴，垂足为E （5分）
由C（-3，8），可知OE=OA=3，
∴AE=AO+OE=6，又CE=8，
∴|AC|=

AE2+CE2

=

62+82

=10（10分）
又AB=BC，OE=OA，
∴OB=

1

2

CE=4．（13分）

点评：本题考查综合应用点的坐标，使用待定系数法求函数的解析式．