题目内容
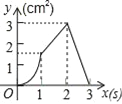
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:

(1)a= ,b= ,c= ;
(2)这个几何体最少由 个小立方体搭成,最多由 个小立方体搭成;
(3)当d=2,e=1,f=2时,画出这个几何体的左视图.
【答案】(1)a=3,b=1,c=1;
(2)这个几何体最少由9个小立方体搭成,最多由11个小立方体搭成;
(3) 左视图如图:

【解析】试题分析:(1)如图从主视图第三列可看出这一列最高的是由三个立方体搭成,再结合俯视图,第三列仅第一行有立方体,所以a=3;从俯视图可看出第二列的第一行、第二行均有立方体,从主视图看出第二列仅一个立方体,则说明b=c=1;(2)从俯视图可看出第一列的第一、二、三行均有立方体,从主视图上看出第一列最高的有两个立方体,则说明可能是d=2,e=f=1或e=2,d=f=1也可能是f=2,e=d=1,也有可能是d=e=f=2,或者e=d=2,f=1、e=f=2,d=1或者d=f=2,e=1;所以最少有3+1+1+1+1+2=9个立方体,最多有3+1+1+6=11个立方体.
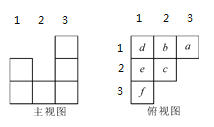
试题解析:(1)如图所示:结合主视图与俯视图可以得到a=3,b=1,c=1.
(2)从主视图和俯视图中可以看出d、e、f中最大为2,所以有以下几种情况:
① d=2,e=f=1② e=2,d=f=1③ f=2,e=d=1,④ e=d=2,f=1⑤ e=f=2,d=1⑥ d=f=2,e=1⑦ d=e=f=2,所以当d、e、f中有一个为2,其他两个为1时,组成几何体的立方体最少为3+1+1+1+1+2=9;当d=e=f=2时,组成几何体的立方体最多为3+1+1+6=11(3)左视图如图所示.

【题目】体育委员统计了全班同学60 s跳绳的次数,并列出频数分布表如下:
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 |
频数 | 2 | 4 | 21 | 13 | 8 | 4 |
(1)全班有多少学生?
(2)组距是多少?组数是多少?