题目内容
【题目】在平面直角坐标系中,点B为第一象限内一点,点A为x轴正半轴上一点,分别连接OB,AB,△AOB为等边三角形,点B的横坐标为4.

(1)如图1,求线段OA的长;
(2)如图2,点M在线段OA上(点M不与点O、点A重合),点N在线段BA的延长线上,连接MB,MN,BM=MN,设OM的长为t,BN的长为d,求d与t的关系式(不要求写出t的取值范围);
(3)在(2)的条件下,点D为第四象限内一点,分别连接OD,MD,ND,△MND为等边三角形,线段MA的垂直平分线交OD的延长线于点E,交MA于点H,连接AE,交ND于点F,连接MF,若MF=AM+![]() AN,求点E的横坐标.
AN,求点E的横坐标.
【答案】(1)8;(2)d=8+t;(3)点E的横坐标为6.
【解析】
(1)过点B作BH⊥OA于点H,根据等边三角形的性质解答即可;
(2)过点M作MP⊥AB于点P,根据等边三角形的性质解答即可;
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,通过等边三角形的性质和全等三角形的性质的到AN=t,OM=t,AH=MH=![]() ,OH=OM+MH=
,OH=OM+MH=![]() ,通过证明AM=AN,可得关于t的方程,求出t,即可得出答案。
,通过证明AM=AN,可得关于t的方程,求出t,即可得出答案。
解:(1)如图,过点B作BH⊥OA于点H,
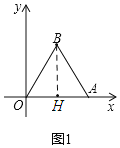
∵△AOB为等边三角形,∴BO=BA,
∵BH⊥OA,∴OH=AH,
∵点B横坐标为4,∴OH=4,
∴OA=2HO=8;
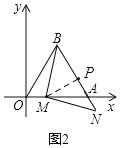
(2)如图,过点M作MP⊥AB于点P,∴∠MPA=90°,
∵BM=MN,∴BP=PN,
∵△AOB为等边三角形,∴BA=AO=8,∠BAO=60°,
∴∠AMP=30°,∴AP=![]() AM,
AM,
∵AM=8﹣t,∴AP=![]() (8﹣t)=4﹣
(8﹣t)=4﹣![]() t,∴BP=AB﹣AP=4+
t,∴BP=AB﹣AP=4+![]() t,
t,
∴BN=2BP=8+t,∴d=8+t
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,
∵△AOB为等边三角形,∴∠BOA=60°=∠OAB,
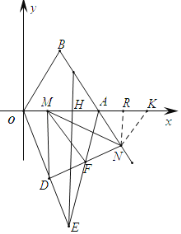
∵NK∥OB,∴∠NKA=∠BOA=60°,且∠OAB=∠NAK=60°,
∴∠NAK=∠NKA=60°,∴△AKN是等边三角形
∴AN=NK=AK,
∵△MND为等边三角形,
∴∠NMD=∠MND=60°,MN=MD,
∴∠OMD+∠NMK=∠NMK+∠MNK=180°﹣60°=120°,
∴∠OMD=∠MNK,
∵AN=8+t﹣8=t,OM=t,
∴OM=AN=NK=AK=t,且∠OMD=∠MNK,MD=MN,
∴△OMD≌△KNM (SAS),
∴OD=MK,∠MOD=∠MKN=60°,
∵MK=﹣t+t=8,∴OD=8,
∵EH垂直平分MA,∴AH=MH=![]() AM=
AM=![]() (8﹣t)=4﹣
(8﹣t)=4﹣![]() t,
t,
∴OH=OM+MH=t+4﹣![]() t=4+
t=4+![]() t,
t,
∵∠OEH=90°﹣60°=30°,∴OE=2HO=8+t,∴DE=8+t﹣8=t,∴DE=AN,
∵∠DOA=∠BAO,∴BN∥OE,∴∠NAF=∠DEF,
又∵∠AFN=∠EFD,AN=DE,∴△AFN≌△EFD(AAS),∴FN=FD,
又∵MN=MD,∴MF⊥DN,
∵NR⊥AK,∴∠ARN=90°,且∠NAK=60°,∴∠ANR=30°,
∴AR=![]() ,
,
∵MR=AM+AR=AM+![]() ,MF=AM+
,MF=AM+![]() ,∴MR=MF,且 MF⊥DN,NR⊥AK,
,∴MR=MF,且 MF⊥DN,NR⊥AK,
∴∠MNR=∠MND=60°,∴∠NMA=90°﹣60°=30°,
∵∠BAO=∠AMN+∠ANM,∴∠AMN=∠ANM=30°,∴AM=AN,∴8﹣t=t,∴t=4,
∴OH=4+![]() ×4=6,∴点E的横坐标为6.
×4=6,∴点E的横坐标为6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案