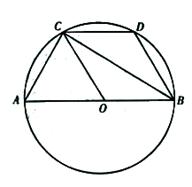
题目内容
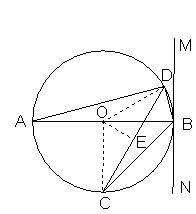
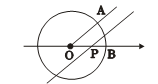
如图,⊙ 的直径
的直径 是
是 ,过
,过 点的直线
点的直线 是⊙
是⊙ 的切线,
的切线,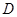 、
、 是⊙
是⊙ 上的两点,连接
上的两点,连接 、
、 、
、 和
和 .
.

(1)求证: ;
;
(2)若 是
是 的平分线,且
的平分线,且 ,求
,求 的长.
的长.
 的直径
的直径 是
是 ,过
,过 点的直线
点的直线 是⊙
是⊙ 的切线,
的切线,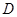 、
、 是⊙
是⊙ 上的两点,连接
上的两点,连接 、
、 、
、 和
和 .
.
(1)求证:
 ;
;(2)若
 是
是 的平分线,且
的平分线,且 ,求
,求 的长.
的长.(1)证明: ∵ 是⊙
是⊙ 的直径
的直径
∴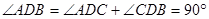
∵ 切⊙
切⊙ 于点
于点
∴
∴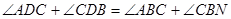
∵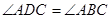
∴ .
.
(2) 如右图,连接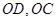 ,过点
,过点 作
作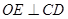 于点
于点 .
.
∵ 平分
平分
∴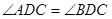
∴弧
 弧
弧
∵ 是⊙
是⊙ 的直径
的直径
∴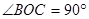
又∵

∴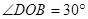
∵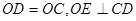
∴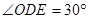
∵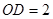
∴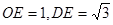
∴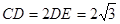 .
.
 是⊙
是⊙ 的直径
的直径∴
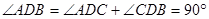
∵
 切⊙
切⊙ 于点
于点
∴

∴
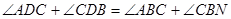
∵
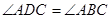
∴
 .
.(2) 如右图,连接
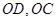 ,过点
,过点 作
作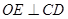 于点
于点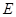 .
.
∵
 平分
平分
∴
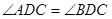
∴弧
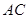
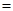 弧
弧
∵
 是⊙
是⊙ 的直径
的直径∴
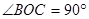
又∵


∴
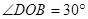
∵
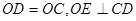
∴
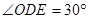
∵
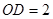
∴
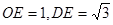
∴
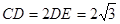 .
.(1)由AB为⊙O的直径,得:∠ADB=90°,根据MN是⊙O的切线,可知:∠AMN=90°,根据同弧所对的圆周角相等,可知:∠ADC=∠ABC,从而证得:∠CBN=∠CDB;
(2)连接OD、OC,过点O作OE⊥CD于点E,根据圆周角定理,可求得∠BOC和∠DOB的度数,故可知:∠COD的度数,在等腰△OCD中,可将CD的长求出.
(2)连接OD、OC,过点O作OE⊥CD于点E,根据圆周角定理,可求得∠BOC和∠DOB的度数,故可知:∠COD的度数,在等腰△OCD中,可将CD的长求出.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 是
是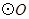 的直径,
的直径,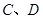 是
是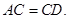
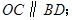
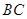 将四边形
将四边形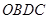 分成面积相等的两个三角形,试确定四边形
分成面积相等的两个三角形,试确定四边形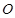 是以数轴的原点
是以数轴的原点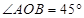 ,点
,点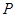 在数轴上运动,若过点
在数轴上运动,若过点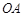 平行的直线与⊙
平行的直线与⊙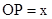 ,则
,则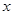 的取值范围是:
的取值范围是: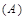 -1≤
-1≤
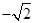 ≤
≤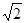
 0≤
0≤
 为坐标原点,点
为坐标原点,点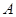 的坐标为
的坐标为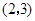 ,
,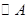 的半径为1,过
的半径为1,过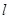 平行于
平行于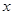 轴,点
轴,点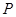 在
在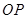 的长.
的长.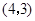 时,试判断直线
时,试判断直线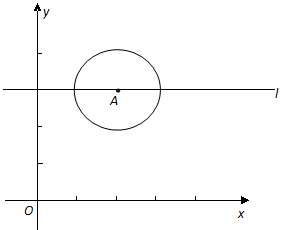
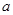 的正
的正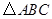 内有一边长为
内有一边长为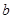 的内接正
的内接正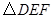 ,则
,则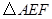 的内切圆半径为 .
的内切圆半径为 .
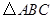 内接于⊙O,
内接于⊙O,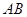 为⊙O的直径,
为⊙O的直径,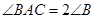 ,
,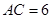 ,过点
,过点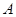 作⊙O的切线与
作⊙O的切线与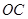 的延长线交于点
的延长线交于点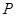 ,求
,求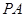 的长.
的长.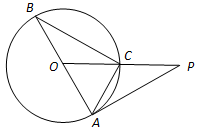
 的正六边形周长为 .
的正六边形周长为 .