题目内容
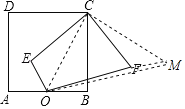
【题目】如图，正方形ABCD的边长为5，O是AB边的中点，点E是正方形内一动点，OE＝2，将线段CE绕C点逆时针旋转90°得CF，连OF，线段OF的最小值为_____．
【答案】
【解析】
如图，连接DO，将线段DO绕点D逆时针旋转90°得DM，连接OF，FM，OM，根据全等三角形的性质得到FM＝OE＝2，根据勾股定理得到OC＝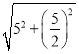
＝
，求得OM=
OC＝，，于是得到结论．
解：如图，连接DO，将线段DO绕点D逆时针旋转90°得DM，连接OF，FM，OM，
∵∠ECF＝∠OCM＝90°，
∴∠ECO＝∠FCM，
∵CE＝CF，CO＝CM，
∴△ECO≌△FCM（SAS），
∴FM＝OE＝2，
∵正方形ABCD中，AB＝5，O是AB边的中点，
∴OB＝2.5，
∴OC＝＝，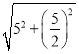
∴OM＝OC＝，
∵OF+MF≥OM，
∴OF≥．
∴线段OF的最小值为．
练习册系列答案
相关题目
