题目内容
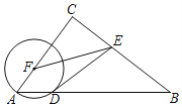
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为_______________.
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为_______________.
【答案】![]()
【解析】
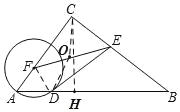
先取EF得中点O,连接DE、DE、DC,所以OC=![]() EF,由AF=DF,BE=DE,得到∠A=∠ADF,∠B=∠BDE,从而∠ADF+∠BDE=∠A+∠B=90°,所以∠EDF=90°,因此OD=
EF,由AF=DF,BE=DE,得到∠A=∠ADF,∠B=∠BDE,从而∠ADF+∠BDE=∠A+∠B=90°,所以∠EDF=90°,因此OD=![]() EF,得到EF=OC+OD,因此当C、O、D三点在同一直线上,且CD⊥AB时,OC+OD最短,由OE=OF,OC=OD,∠C=90°得到四边形CEDF为矩形,于是过点C作CH⊥AB,此时点D与H重合,EF=OC+OD=CD=CH最短,由∠AFD=∠BED=90°,可知∠A=∠B=45°,从而CH为
EF,得到EF=OC+OD,因此当C、O、D三点在同一直线上,且CD⊥AB时,OC+OD最短,由OE=OF,OC=OD,∠C=90°得到四边形CEDF为矩形,于是过点C作CH⊥AB,此时点D与H重合,EF=OC+OD=CD=CH最短,由∠AFD=∠BED=90°,可知∠A=∠B=45°,从而CH为![]() AB=
AB=![]() ,故EF的最小值为
,故EF的最小值为![]()
取EF得中点O,连接DE、DE、DC,
∵∠C=90°,
∴OC=![]() EF,∠A+∠B=90°,
EF,∠A+∠B=90°,
∵AF=DF,BE=DE,
∴∠A=∠ADF,∠B=∠BDE,
∴∠ADF+∠BDE=∠A+∠B=90°,
∴∠EDF=90°,
∴OD=![]() EF,
EF,
∴EF=OC+OD,
当C. O、D三点在同一直线上,且CD⊥AB时,OC+OD最短,
∵OE=OF,OC=OD,
∴四边形CEDF为平行四边形,
∵∠C=90°,
∴四边形CEDF为矩形,
于是过点C作CH⊥AB,此时点D与H重合,EF=OC+OD=CD=CH最短,
∴∠AFD=∠BED=90°,
∴∠A=∠B=45°,
CH=![]() AB=
AB=![]() ,
,
∴EF的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目