Question

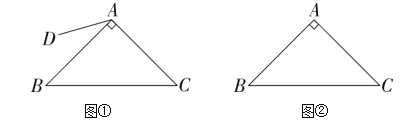
【题目】在菱形ABCD中，AC于BD交于点O，过点O的MN分到交AB、CD于M、N．

（1）求证：AM＋DN＝AD；

（2）∠AOM＝∠OBC，AC＝2，BD＝2，求MN的长度．

Answer 1

【答案】（1）见解析；（2）2.

【解析】

（1）证明△AOM≌△CON，可得结论；

（2）证明△AOM∽△ABO，列比例式：，可得OM的长，由MN＝2OM，代入可得MN的长．

（1）证明：∵四边形ABCD是菱形，

∴AO=OC，AB∥CD，AD=CD，

∴∠MAC=∠NCA，

∵∠AOM=∠CON，

∴△AOM≌△CON，

∴AM=CN，

∴DC=DN+CN=DN+AM，

∴AD=AM+DN；

（2）解：∵四边形ABCD是菱形，

∴∠ABO=∠OBC，AC⊥BD

∵ AC＝2，BD＝2，

∴ AO＝，OB＝，

由勾股定理得：，

∵∠AOM=∠OBC，

∴∠ABO=∠AOM，

∵∠BAO=∠MAO，

∴△AOM∽△ABO，

∴，

∴，

∴，

∴．