题目内容
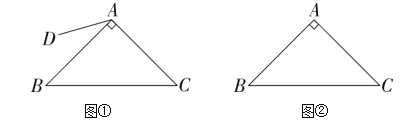
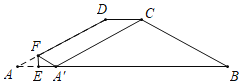
【题目】如图,在四边形纸片ABCD中,AB=10,CD=2,AD=BC=5,∠A=∠B,现将纸片沿EF折叠,使点A的对应点A′落在边AB上,连接A′C,如果△A′BC恰好是以AC为腰的等腰三角形,则AE的长是___.
【答案】1或![]() .
.
【解析】
如图1,过点C作CM⊥AB于点M,过点D作DN⊥AB于点N,则易证△ADN≌△BCM,进一步可求得AN=BM=4;由于△A′BC恰好是以AC为腰的等腰三角形,故可分两种情况考虑:若A'C=BC,如图1,由等腰三角形的性质可得BM=A'M=4,进一步即可求出AE的长;若A'C=A'B,如图2,由CM 是两个直角△![]() 、△
、△![]() 的公共边,根据勾股定理可得CM2=BC2﹣BM2=A'C2﹣A'M2,再代入数据求解方程即可.
的公共边,根据勾股定理可得CM2=BC2﹣BM2=A'C2﹣A'M2,再代入数据求解方程即可.
解:如图1,过点C作CM⊥AB于点M,过点D作DN⊥AB于点N,
在△ADN和△BCM中,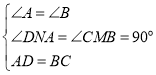 ,
,
∴△ADN≌△BCM(AAS)
∴AN=BM,DN=CM,且DN∥CM,
∴四边形DCMN是矩形,
∴CD=MN=2
∴AN=BM=![]() ,
,
∵将纸片沿EF折叠,使点A的对应点A'落在AB边上,
∴AE=A'E,
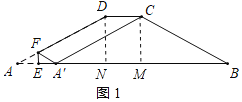
若A'C=BC,
∵CM⊥AB,
∴BM=A'M=4,
∴AA'=AB﹣A'B=10﹣8=2,
∴AE=1,
若A'C=A'B,如图2所示:
∵CM2=BC2﹣BM2=A'C2﹣A'M2,
∴25﹣16=A'B2﹣(4﹣A'B)2,
解得:A'B=![]() ,
,
∴AA'=AB﹣A'B=10﹣![]() =
=![]() ,
,
∴AE=![]() AA'=
AA'=![]() ;
;
故答案为:1或![]() .
.


练习册系列答案
相关题目