题目内容
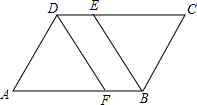 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.
分析:AF应该和CE相等,可通过证明三角形ADF和三角形BEC全等来实现.根据平行四边形的性质我们可得出:AD=BC,∠A=∠C,∠ADC=∠ABC,因为DF和BE是∠ADC,∠CBA的平分线,那么不难得出∠ADF=∠CBE,这样就有了两角夹一边,就能得出两三角形全等了.
解答:解:AF=CE.理由如下:
∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,∠ADC=∠ABC,
又∵∠ADF=
∠ADC,∠CBE=
∠ABC,
∴∠ADF=∠CBE,
在△ADF和△CBE中,
∴△ADF≌△CBE(ASA),
∴AF=CE.
∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,∠ADC=∠ABC,
又∵∠ADF=
| 1 |
| 2 |
| 1 |
| 2 |

∴∠ADF=∠CBE,
在△ADF和△CBE中,
|
∴△ADF≌△CBE(ASA),
∴AF=CE.
点评:求某两条条线段相等,可通过证明他们所在的三角形全等来实现,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为