题目内容
【题目】如图，在Rt△ABC中，∠BAC＝90°，∠C＝50°，AH，BD分别是△ABC高和角平分线，点P为边BC上一个点，当△BDP为直角三角形时，则∠CDP＝_____度．
【答案】40或20．
【解析】
直接根据三角形内角和定理得∠ABC＝40°，由角平分线的定义得∠DBC＝20°，当△BDP为直角三角形时，存在两种情况：分别根据三角形外角的性质即可得出结论．
解：∵∠BAC＝90°，∠C＝50°，
∴∠ABC＝90°﹣50°＝40°
∵BD平分∠ABC
∴∠DBC＝
＝20°
当△BDP为直角三角形时，有以下两种情况：
①当∠BPD＝90°时，如图1，
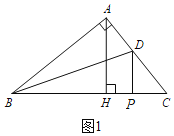
∵∠C＝90°，
∴∠CDP＝90°﹣50°＝40°；
②当∠BDP＝90°时，如图2，
∴∠BPD＝90°﹣20°＝70°，
∵∠BPD＝∠C+∠CDP，
∴∠CDP＝70°﹣50°＝20°，
综上，∠CDP的度数为40°或20°．
故答案为：40或20．
阅读快车系列答案【题目】某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”．下面表中是小张和小王两位同学的成绩记录：
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
（1）若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；
（2）若按完成作业、单元检测、期末考试三项成绩按
的权重来确定期末评价成绩．
①请计算小张的期末评价成绩为多少分？
②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？
【题目】安庆市在精准扶贫活动中，因地制宜指导农民调整种植结构，增加种植效益，2018年李大伯家在工作队的帮助下，计划种植马铃薯和蔬菜共15亩，预计每亩的投入与产出如下表：（每亩产出-每亩投入=每亩纯收入）
种类 | 投入（元） | 产出（元） |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
（1）如果这15亩地的纯收入要达到54900元，需种植马铃薯和蔬菜各多少亩？
（2）如果总投入不超过16000元，则最多种植蔬菜多少亩？该情况下15亩地的纯收入是多少？
