��Ŀ����
����Ŀ��Ŀǰ���С�У�ֻ�������Խ��Խ�ܵ�����ע�����������������һ�г�����1������ѧ��ȤС���ͬѧ���������ѧУ�������ҳ��ԡ���ѧ�����ֻ��������̬�ȣ�̬�ȷ�Ϊ��A������ν��B�������ɣ�C���ɣ�D�����ԣ����������������Ƴ�Ƶ������ͳ��ͼ1������ͳ��ͼ2�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������˶�������ѧ���ҳ���
��2�����ͼ2������C���Ե�Բ�ĽǵĶ���������ͼ1����������
��3�����ݳ��������������������У11000����ѧ���ҳ����ж������ҳ��ַ���̬�ȣ�
��4���ڴ˴ε����У�������1����ͳ�����2�������2λ�ҳ�����ѧ�����ֻ��ַ���̬�ȣ��ִ���ѡ2λ�ҳ��μ�ѧУ��֯�ļ�У������б�������״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
���𰸡�
��1���⣺���������ѧ���ҳ����ǣ�40��20%=200���ˣ�
��2���⣺����C���Ե�Բ�ĽǵĶ����ǣ�
360�����1��20%��15%��60%��=18�㣻
C��������ǣ�200����1��20%��15%��60%��=10���ˣ���
��ͼ���£�

��3���⣺��������ã�
11000��60%=6600���ˣ���
����У11000����ѧ���ҳ�����6600���ҳ��ַ���̬��
��4���⣺�������1���������ҳ�ΪA1��A2��������2���������ҳ�ΪB1��B2��
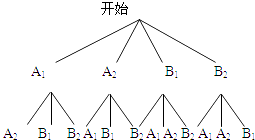
һ����12�ֵȿ��ܽ��������2�����Բ�ͬ�༶����8��
��P��2�����Բ�ͬ�༶��= ![]() =
= ![]() ��
��
����������1���۲�����ͳ��ͼ������ͳ��ͼ����B������������������ѧ���ҳ�����
��2�������C��ռ�İٷֱȣ������������C���Ե�Բ�ĽǵĶ������ٷֱ����C���D������������ɲ�ȫ����ͳ��ͼ��
��3������У��ѧ���ҳ�����������D��ռ�ٷֱȼ��ɡ�
��4���г���״ͼ�����ݸ��ʹ�ʽ�������ѡ����2�����Բ�ͬ�༶�ĸ��ʡ�
�����㾫����ͨ�������������ͳ��ͼ������ͳ��ͼ������������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ط�ӳ����ı仯��������Dz�������ر�ʾ������������ռ�İٷֱȼ����Խ����⣮

 ������������ϵ�д�
������������ϵ�д�




