��Ŀ����
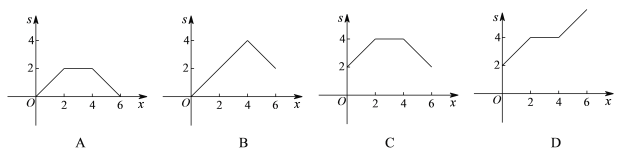
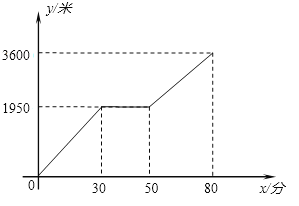
����Ŀ��С����С����ɽ���棬С�����У�С�������³�����Լ��ɽ���³����յ���. ��֪С���i�е�·�����³�������·����2����С����С��������50���Ӳ������³����³���ƽ���ٶ�Ϊÿ����180��. ͼ�е����߷�ӳ��С�����ߵ�·��![]() ���ף���ʱ��
���ף���ʱ��![]() �����ӣ�֮��ĺ�����ϵ.
�����ӣ�֮��ĺ�����ϵ.
��1��С�����ߵ���·����___________�ף���;����Ϣ��___________���ӣ�С����Ϣ֮�����ߵ��ٶ���ÿ����___________�ף�
��2����![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��___________.
�ĺ�����ϵʽ��___________.
��3����С�������³��յ�ʱ��С�����³��յ��·����___________��.
���𰸡���1��3600��20��55����2��y=65x����3��1100
��������
����ͼ���ȡ��Ϣ��
��1��С������ɽ����ʱ80���ӣ���;��Ϣ��20���ӣ��г�Ϊ3600�ף���Ϣǰ30��������1950�ף���Ϣ��30�������ߣ�3600-1950���ף�����·�̡�ʱ��ó��ٶȼ��ɣ�
��2�����ô���ϵ���������������������ʽ���ɣ�
��3����С�������³��յ��ʱ�䣬����С������·�̣������³��յ��·�̣�
�⣺��1������ͼ��֪��С�����ߵ���·���� 3600�ף���;����Ϣ�� 20���ӣ�С����Ϣ֮�����ߵ��ٶ��ǣ�3600-1950������80-50��=55��/���ӣ�
�ʴ�Ϊ 3600��20��55��
��2���躯����ϵʽΪy=kx��
�ɵã�1950=30k��
��ã�k=65��
���Խ���ʽΪ��y=65x��
�ʴ�Ϊ��y=65x��
��3��С������ʱ�䣺![]() ��
��
С������ɽ����ʱ80���ӣ�
С����С���ٵ�80-50-10=20���֣���
��С�������յ�ʱ��С�����³��յ��·��Ϊ��20��55=1100���ף���
�ʴ�Ϊ��1100��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�