题目内容
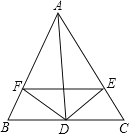
【题目】如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
A.①②③B.①③④C.①②④D.②③④
【答案】A
【解析】
根据角平分线的性质得到DE=DF,根据垂直的定义、等腰三角形的性质判断①;根据线段垂直平分线的判定定理判断②;根据三角形的面积公式判断③,结合题意判断④.
解:∵∠A的平分线交BC于D,DE⊥AC,DF⊥AB,
∴DE=DF,
∴∠DEF=∠DFE,又∠AED=∠AFD=90°,
∴∠AEF=∠AFE,①正确;
∵∠AEF=∠AFE,
∴AE=AF,又DE=DF,
∴AD垂直平分EF,②正确;
S△BFD:S△CED=![]() ×BF×DF:
×BF×DF:![]() ×CE×DE=BF:CE,③正确;
×CE×DE=BF:CE,③正确;
EF与BC不一定平行,④错误,
故选:A.

练习册系列答案
相关题目