题目内容
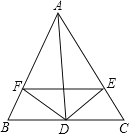
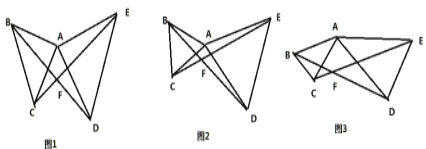
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
【答案】(1)90°;(2)60°;(3)![]() 证明见解析;
证明见解析;
【解析】
(1)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(2)求出![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(3)根据![]() 根据SAS证出
根据SAS证出![]() ≌
≌![]() 即可.
即可.
(1)如图:
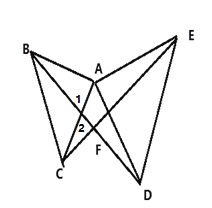
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
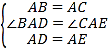 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:90°
(2)如图:
∵△ABC和△ADE都是等边三角形
∴AD=AE,AB=AC,![]()
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
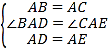 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
故答案为:60°
(3) ![]() 理由如下:
理由如下:
∵∠BAC=∠DAE
又∵![]()
∴∠DAB=∠EAC,
∵在△ADB和△AEC中
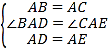 ,
,
∴△ADB≌△AEC(SAS),
∴![]()
∴![]()

【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数解析式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.