题目内容
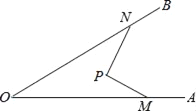
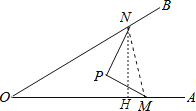
【题目】如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=![]() ,ON=8,则OM=_____.
,ON=8,则OM=_____.
【答案】4![]() +2
+2
【解析】
连结MN,作NH⊥OA于H,如图,根据旋转的性质得∠MPN=90°,PN=PM=![]() ,可判断△PMN为等腰直角三角形,则MN=
,可判断△PMN为等腰直角三角形,则MN=![]() PM=2
PM=2![]() ,在Rt△OHN中,根据含30度的直角三角形三边的关系得NH=
,在Rt△OHN中,根据含30度的直角三角形三边的关系得NH=![]() ON=4,OH=
ON=4,OH=![]() NH=4
NH=4![]() ,然后在Rt△MNH中根据勾股定理计算出MH=2,由此得到OM=OH+HM=4
,然后在Rt△MNH中根据勾股定理计算出MH=2,由此得到OM=OH+HM=4![]() +2.
+2.
连结MN,作NH⊥OA于H,如图,
∵线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点,
∴∠MPN=90°,PN=PM=![]() ,
,
∴△PMN为等腰直角三角形,
∴MN=![]() PM=2
PM=2![]() ,
,
在Rt△OHN中,∵∠NOH=30°,ON=8,
∴NH=![]() ON=4,
ON=4,
OH=![]() NH=4
NH=4![]() ,
,
在Rt△MNH中,∵NH=4,MN=2![]() ,
,
∴MH=![]() =2,
=2,
∴OM=OH+HM=4![]() +2.
+2.
故答案为4![]() +2.
+2.

练习册系列答案
相关题目
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.